25 | 毕业设计：用O(1)的时间复杂度计算整数末尾0的数量

你好，我是胡光。今天是进阶篇的最后一节课了，首先，我们恭喜坚持学到这里的同学，你马上就要从这门课毕业了。在正式毕业之前，为了能让你将前面所学的内容应用起来，学以致用，这节课我们会一起来完成一个实战题目。

我们先来看今天要解决的问题：在$O(1)$的时间复杂度内，求一个以二进制表示的整数末尾有多少个0。

如果没有时间复杂度的限制，这个问题看上去非常地简单，我们只需要按照下面这么做，最后count就是末尾0的计数。这个方法的时间复杂度是$O(\log_2N)$，它和我们所要求的时间复杂度相去甚远，而且这个解法也远远达不到我们毕业设计的要求。这该怎么办呢？

while ((n & (1 << count)) == 0) {
    count += 1;
    }

我们继续来看这个题，既然是想要求这个整数二进制表示末尾有多少个0，那我们是不是可以将这个整数二进制表示的最后一个1取出来。比如说，一个数的二进制表示是101001000，我们就取出1000，设最终0的个数是count，那取出最后一个1，我们得到的数一定是$2^{count}$，我们直接对这个数使用math库里面的函数取对数，或者干脆用哈希表来存储，每次查表就可以了。这个方法看起来是可行的，那么我们要解决的问题就是，怎样得到二进制表示的最后一个1。在讲具体的解决方法之前，我们先来复习一下计算机中存储整数的方式，看看能不能从中得到启发。

计算机中存储整数的3种方式

在之前的课程中我们讲过，有符号的整数在计算机中存储的方式是最高位是符号位，0为正数，1为负数，后面的31bit存储的是这个数的真值。我们前面的例子中，也都是以正整数为例。但实际上，计算机在存储数据的时候还有其他的形式， 也就是我们接下来讲的3种方式。

1. 原码：数字转换成二进制就是原码，只是正数的符号位是0，负数的符号位是1。
2. 反码：正数的反码是它本身，负数的反码是除符号位外全部取反。
3. 补码：正数的补码是它本身，负数的补码是反码加1。

我们以8bit长度的整数为例，分别来看看18和-18的原码、反码和补码：

那你可能要问了，计算机为什么要把事情搞得这么麻烦呢？直接用原码不就可以了吗？这是因为，虽然我们在对整数做运算的时候有基础的四则运算，以及各种各样的数学运算，但计算机远远没有我们这么聪明，它只能做加法运算。计算机的四则运算和取模运算，都是依靠加法运算来实现的，反码和补码就是这种限制之下的产物。

换句话说，我们在原码整数上，直接进行加法是完全没有问题的，但如果正数和负数的原码直接相加就会出现问题。比如说，在上面的例子中，18和-18相加应该等于0，但如果我们直接使用原码相加就会等于-36，使用反码相加就会变成-127。使用补码相加会稍微复杂一些，因为补码中是以最低位的1为分界线，高位全都互反，而低位全都是0，两个数相加之后，会把前面有效位上的1全都抵消掉，最终结果就是0。我们发现，只有使用补码的方式才能得到正确的计算结果。

我们再看一个补码的计算例子，这次，我们要计算18-5，在计算机中就是18+(-5)，而18的补码表示是0 0010010，-5的补码表示是1 1111011，最终的结果0 0001101也就是13。

因此，补码的存在使得四则运算变成了可能，所有的数在计算机中的存储方式也都应用了补码。

利用补码之后，我们要解决的题目就变得简单得多了。对于正整数x，它在计算机中的存储是它本身的二进制表示，而-x在计算机中的存储则是将它取反之后再加上1，即-x+1。一个数取反之后，它的二进制表示中，最低位的那个1会变成0，从它往低全都变成了1，而加1之后，最低位1的那个bit还会变成1，从它往低又全都变成了0。

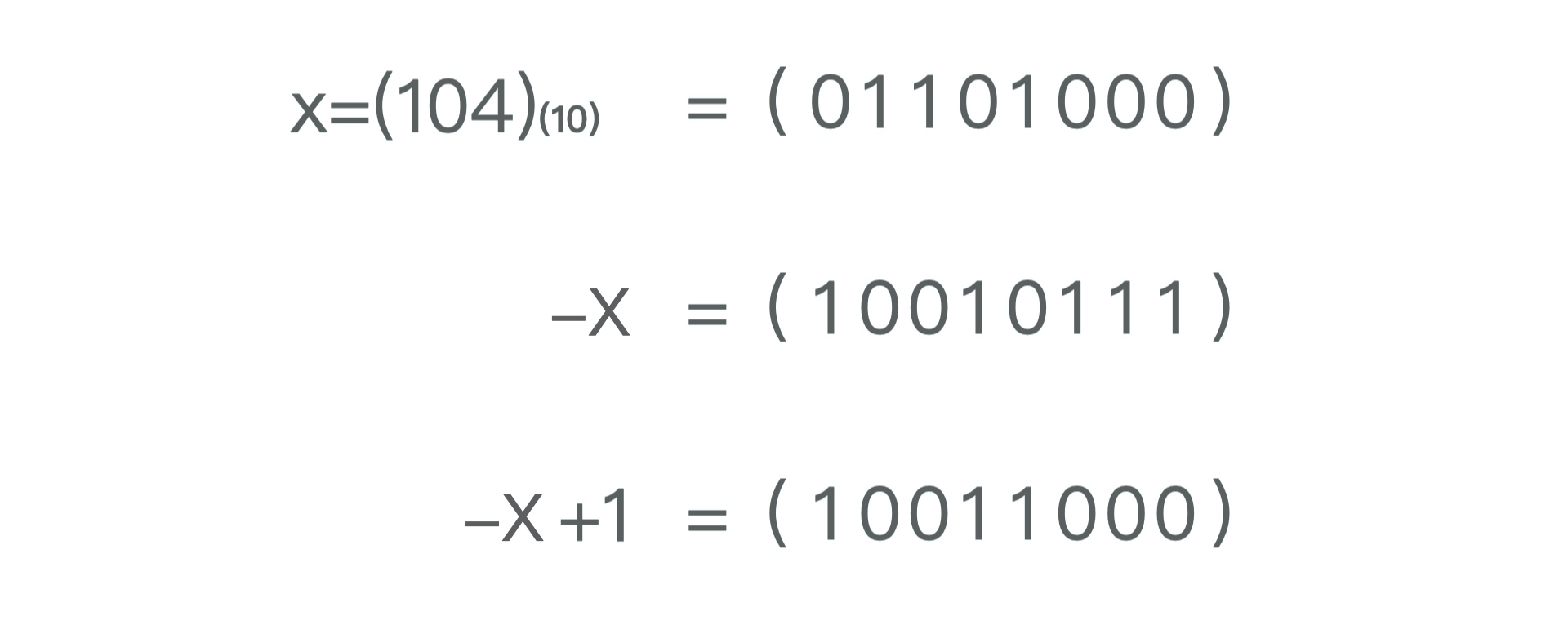
也就是说，x和-x在计算机中的表示，以x的二进制表示中最低位的1为界，从它开始，低位全都一样，高位全都互反，所以我们可以通过x & (-x)，就能取出最低位1。这样一来，我们就能得到我们今天题目的最终解决代码log2(n & (-n));。

这个时候看上去，我们已经实现了题目的要求，但无论是去对数操作还是去查哈希表，实际上它们都不算是快速的原子操作，就算是$O(1)$和$O(1)$之间也是有区别的。那你可能要问了，都是$O(1)$为什么还要在乎那点儿区别呢？当然要在乎，例如在游戏领域中需要高时效、频繁调用的时候，一点细微的差别对用户来讲都是很显著的差异。那么针对这个问题，我们有没有更快的解决方法呢？

De Bruijn序列

你还记得，上节课我们在求sqrt的时候，最后讲到的那一段代码吗？在那一段代码中，我们用了真$O(1)$的时间复杂度求得了结果，但是也得到了一个永久的谜团：0x5F3759DF到底是啥。今天，我们再来见证来自斯坦福的另一股神秘力量，位扫描解法：

unsigned int v; // find the number of trailing zeros in 32-bit v
    int r; // result goes here
    static const int MultiplyDeBruijnBitPosition[32] =
    {
    0, 1, 28, 2, 29, 14, 24, 3, 30, 22, 20, 15, 25, 17, 4, 8,
    31, 27, 13, 23, 21, 19, 16, 7, 26, 12, 18, 6, 11, 5, 10, 9
    };
    r = MultiplyDeBruijnBitPosition[((uint32_t)((v & -v) * 0x077CB531U)) >> 27];

利用这一段代码，我们就可以在真$O(1)$的时间复杂度下，求出一个整数的二进制表示中末尾有多少个0。不过，这一段代码中又出现了一个神秘的常量：0x077CB531。现在，我们就来研究一下这个常量是怎么来的。

首先，一个整数是以32bit的长度存储在计算机中的，如果不算符号位，它的最高5位，一共有多少种情况呢？自然是32种情况，从00000到11111。我们将常量0x077CB531展开成二进制表示，就是00000111011111001011010100110001。我们将它看作是一个循环的圆，然后从中依次取出相邻的5个bit，如下图：

这个时候，我们就发现了一个问题，我们取出的这些数刚好是从00000到11111的所有数，既没有重复，也没有遗漏。这样的序列被称作_De Bruijn_序列。它的定义是，B(n, k)为n个元素组成的一个循环序列，在这个循环序列中所有长度为k，且由n个元素构成的序列都在它的子序列中，且仅出现一次，那0x077CB531这个常量的二进制表示就是B(2, 5)的一个序列。

上面的代码我们就可以这样来解释：我们去看这个常量乘上了一个$2^x$之后，它的前5bit是什么。由于这个常量中，每一个长度为5的窗口互相之间都是不一样的，或者说，每一个长度为5的窗口都只对应了一个x，因此，它们就可以用一个长度为32的数组存储起来了。

这样一来，当我们将整数n最低位的1取出与常量相乘，再查看它前5位的时候，直接查表就可以找到那个对应的x，即n的二进制表示中末尾0的位置。

这么说你可能还不理解，我们来看一个具体的例子。比如说整数104，经过计算就是104 & \-104 = 8，也就是1000，因为8=2^3，所以需要把它左移3位：

我们看到它的前五位是00111=7，查表可以看到MultiplyDeBruijnBitPosition[7]=3，结果是正确的。那如果左移超过了27位呢？其实也没有关系，这个常量的前5位都是0，左移也是用0来补低位，所以刚好形成了循环。

上面我们解释了这个常量的意义，那根据这个常量的意义，接下来我们就要来看，这个常量我们可以用什么样的方式来得到呢？

遇事不决用搜索，至少搜索能够帮助我们尝试出下面这种可能性。

首先还是要确定状态。想要构造出来这样一个常量，最基本的单元就是那个长度为5的窗口，也就是说，这个问题里面有32种状态。接下来状态转移：我们从一个窗口转移到相邻的另一个窗口是什么样的操作呢？自然就是左移一位之后在最右边补一个0或者1，或者右移一位之后在最左边补一个0或者1。所以，在这些状态中，如果某一个状态u的前4位和另一个状态v的后4位是一样的就可以转移。比如，10001和00011就是可以转移的，只考虑向右侧补位可以连边的话，我们就能得到一个图，这个图就叫做_De Bruijn图_，我们用一个简单的版本B(2, 3)为例：

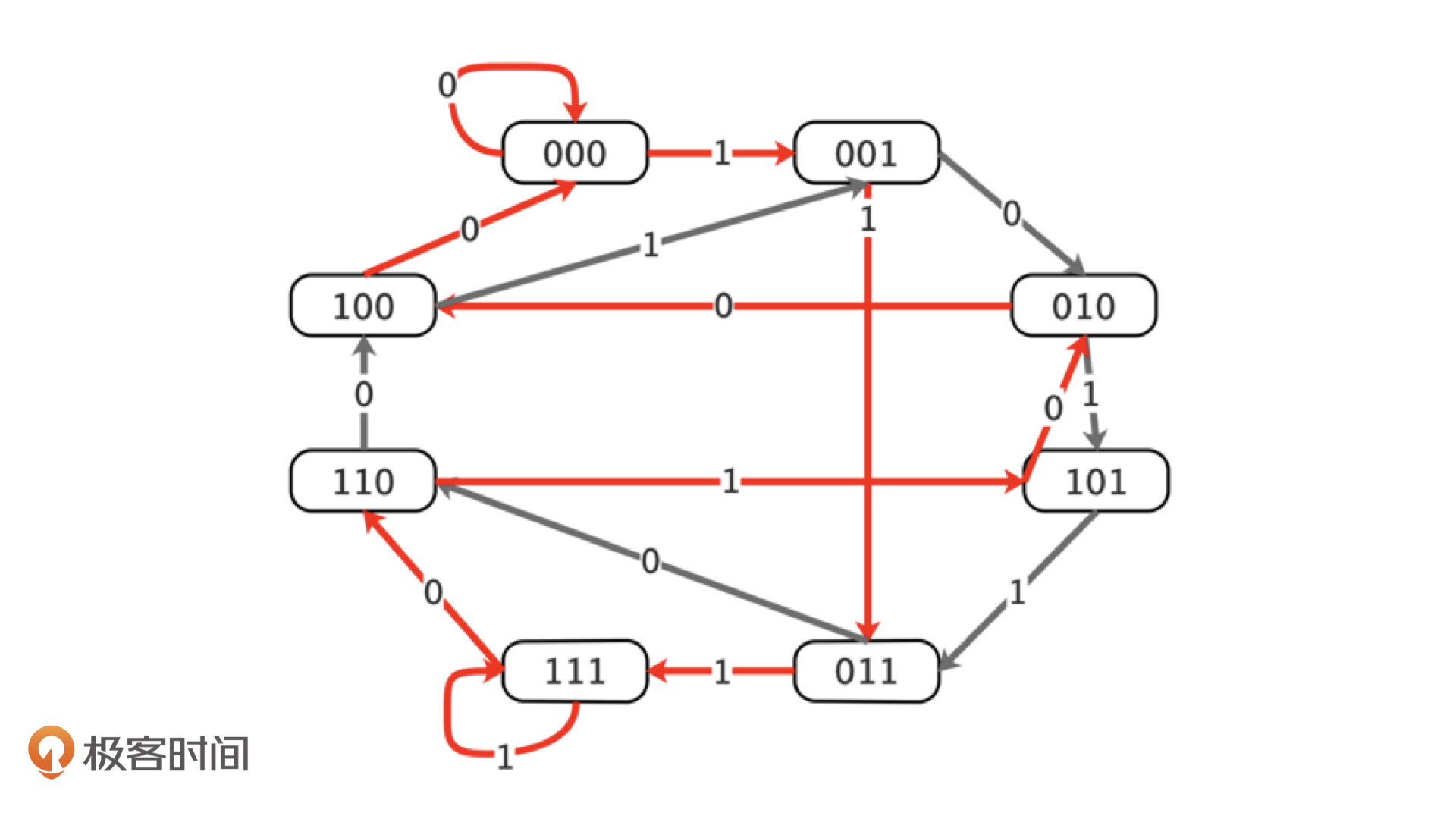
接下来，我们只需要找到一条回路，即这条路的起点到终点都一样，且途经这个图中所有的点一次。也就是说，我们如果在这个图中找到一条汉密尔顿回路（上图中红色的箭头），就可以构造出来一个常量。

很遗憾，汉密尔顿回路问题是一个NP完全问题。也就是说，我们没有有效的方法能够快速找出它（该问题不存在多项式时间解法）。这该怎么办呢？我们可以把图中的思路稍微修改一下，如果我们把状态值和状态转移上补位的那一个数，直接变成边的编号呢？比如000和001之间的那条边，我们就编号成为0001 =1，101到011就编号成为如下图：

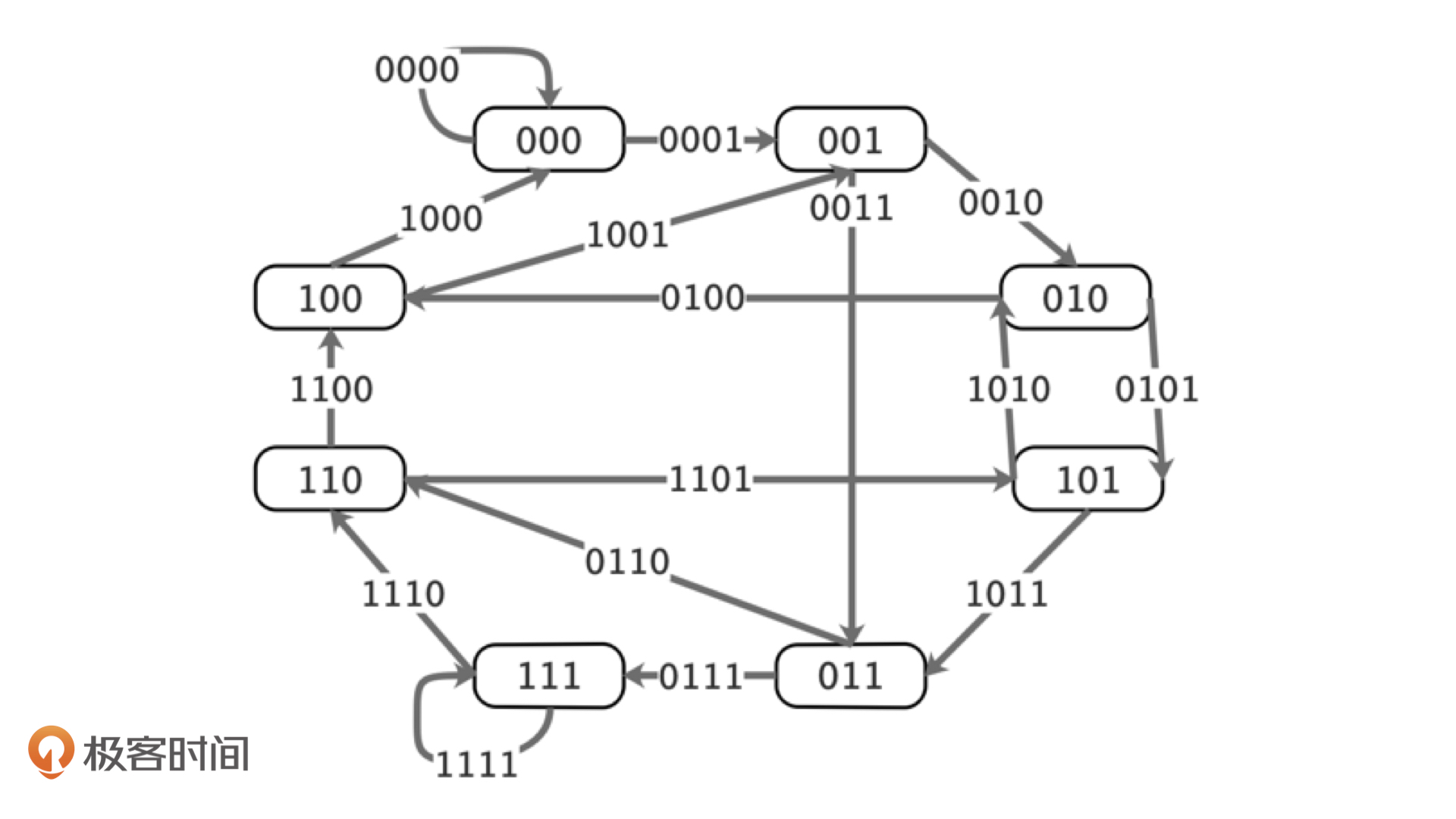
我们发现，图里面刚好有16($2^4$)条边，而且每一个边的编号还都是不一样的，它们刚好对应了窗口为4的所有情况。这是不是就说明，如果我们能够找到一条回路，它途径这个图中所有的边一次，就找到了一个新的序列B(2, 4)呢？没错，这个回路就是欧拉回路。而欧拉回路就有比较快速的解决方法了。欧拉回路的具体概念你可以课后自己去深入学习，对于今天的问题，我们只需要了解到这里就可以了。

由此，我们就能看出来一个规律，就是B(n, k)对应的汉密尔顿回路和B(n, k \- 1)对应的欧拉回路是等价的。回归到今天的问题中，我们想找到那个神秘的常量，只需要找到B(2, 4)对应的图中的欧拉回路就可以了。

小结

今天，我们一起解决一个问题，就是在$O(1)$的时间复杂度内，求出一个以二进制表示的整数末尾有多少个0。

为了解决这个问题，我们先复习了计算机中存储整数的三种方式，分别是原码、反码和补码。利用它们，我们就能快速地找出整数的二进制表示中最低位的1了，然后我们针对$O(1)$的时间复杂度，提出了取对数和哈希表两种常规方案。

最后，我又通过斯坦福大学的位扫描解法，为你详细讲解了De Bruijn序列和求取De Bruijn序列的De Bruijn图。我们通过De Bruijn序列的特殊性质，完成了效率更高的$O(1)$解法，希望你能够通过这个例子，学会其中所蕴含的算法思维。

课后练习

最后，我希望你能自己来完成这个问题的求解流程，为我们整个课程的画上一个完美的句号。

好了，今天的内容就到这里，欢迎你把实现的求解流程写到留言区，我是胡光，我们下节课见！