15 | AVL树:如何让二叉排序树永远保持最优?
你好,我是胡光。
上节课,我们学习了二叉排序树,并且利用它解决了动态查找第k大元素的问题。但是这还不够,因为二叉排序树中存在退化现象,极端情况下,二叉排序树的操作效率并不会比线性表高。虽然我们也学习了最优二叉排序树的求解算法,但是它的代价依旧不低。
为了解决这个问题啊,曾经也有人提出来过,在维护一个动态更新的有序序列的时候,我们先不管二叉排序树是否是最优的,只要是在维护过程中树高超出了一定的限制(如$5\times log_2N$),我们就重新求解二叉排序树。
这是一种比较折中的办法,但仍然要我们间歇性花费不低的代价去保持树的效率。那么有没有什么办法,能够让二叉排序树拥有自适应的能力,在每一次插入、删除之后可以随时调整自己,让自己保持最优状态呢?
当然是有办法的,早在1962年,就有两位数学家提出来了一种方法,这种方法可以做到在二叉排序树上进行增、删、查,以及查找动态第k大元素等操作,时间复杂度都是$O(log_2N)$,这个方法就叫做平衡树,也叫做AVL树。
在平衡树中,“平衡”的意思,就是将二叉树左右两棵子树的高度看作是这两棵树的重量,把这两个重量放在一个天平上,尽可能保持这个天平是平衡的。也就是说,一棵平衡树的左右两棵子树的树高之差不会超过1。由此我们知道,平衡树就是一个最优的二叉排序树,平衡树的树高也就一直保持在$log_2N$左右(实际上是在$log_2(N+1)$和$1.4405\times log_2(N+2)-0.3277$之间)。正因为维持了树高,所以一棵有N个节点的平衡树,每一个操作的时间复杂度都可保持在$O(log_2N)$。
在正式讲平衡树之前,我们还要引入二叉树上的一个关键的操作,旋转(Rotate)操作,这个操作也是平衡树能够改变形态、保持平衡的关键。
二叉树的旋转:二叉树自适应能力的关键
旋转操作的字面意思,就是将二叉树转了一下。旋转后的二叉排序树也依然会保持二叉排序树的性质。也就是说,我们在进行了一次旋转操作之后,最终的产物仍然是一棵二叉排序树,这棵二叉树排序上的每一个节点,总是大于它的左孩子,小于右孩子,而且中序遍历后的结果也保持不变。
树的旋转究竟是怎么操作的呢?打个比方,我们可以把树上的每一个节点看作是弹珠,每一条边看作是绳子。平常这棵树,我们都是用手拎着它的根节点那颗弹珠,让其他的弹珠自然垂下。然后我们有一天突发奇想,想要换一颗弹珠来拎着,比如我们想要拎根的左子节点那颗弹珠,然后让其他的弹珠继续自然垂下。这样,左子节点成为了新的树根,而根节点成为了新树根的右子节点。
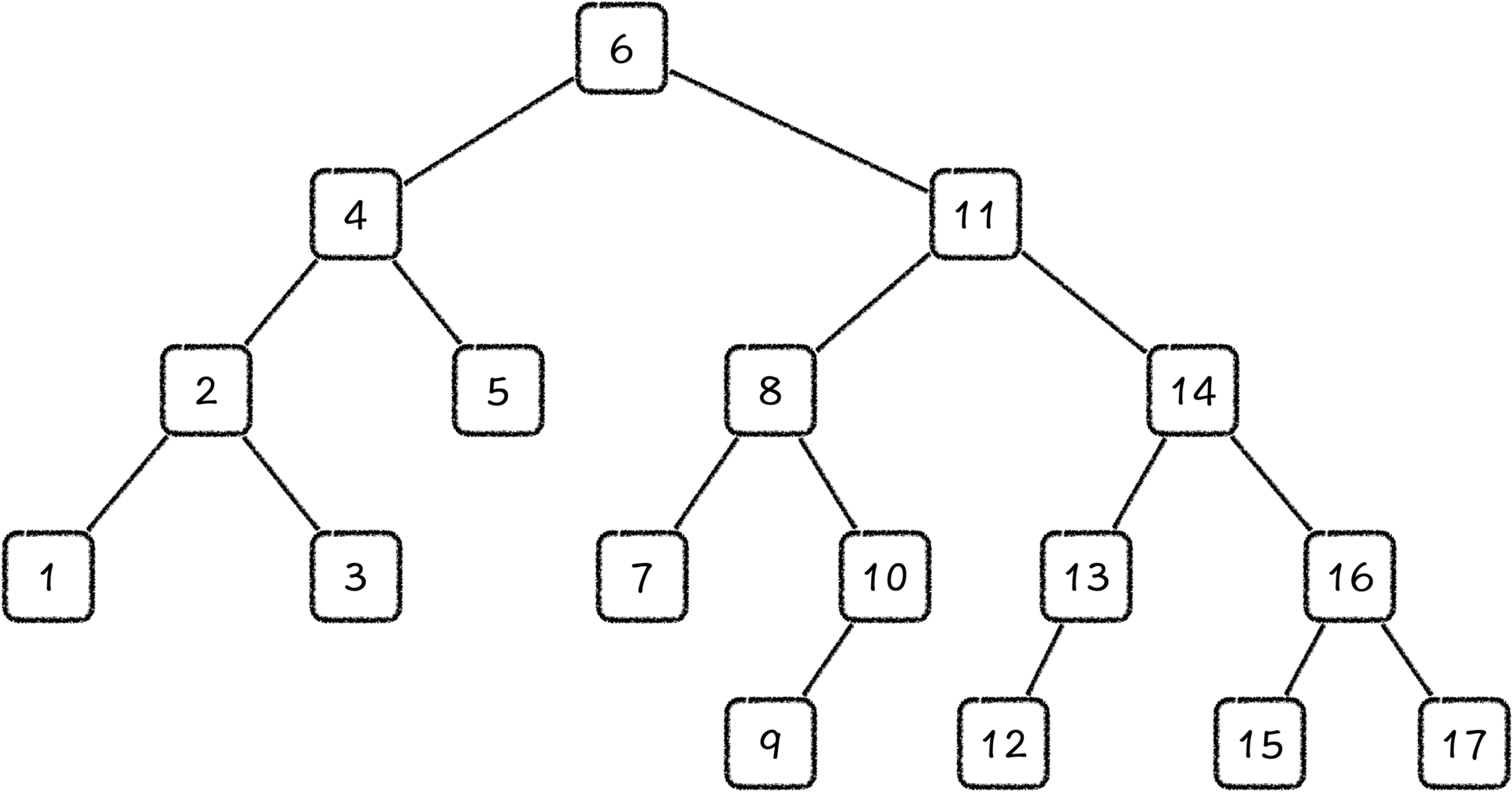
但是,只是这么简单的操作是不够的。如果我们把图1中左子节点,也就是4当作根节点,最终的结果就是节点4除了原有的两个子节点之外,根节点也成为了它的子节点,那它就有3个孩子节点,这显然就不符合二叉树的定义了。所以我们还要进一步明确旋转的细节。
我们把这个问题放到一个比较简单,但却足以代表所有情况的例子中。如下图中左边这棵树,我们将它按照上面描述的方式进行了一次操作之后,2变成了根节点,1、3、4都变成了它的孩子节点。
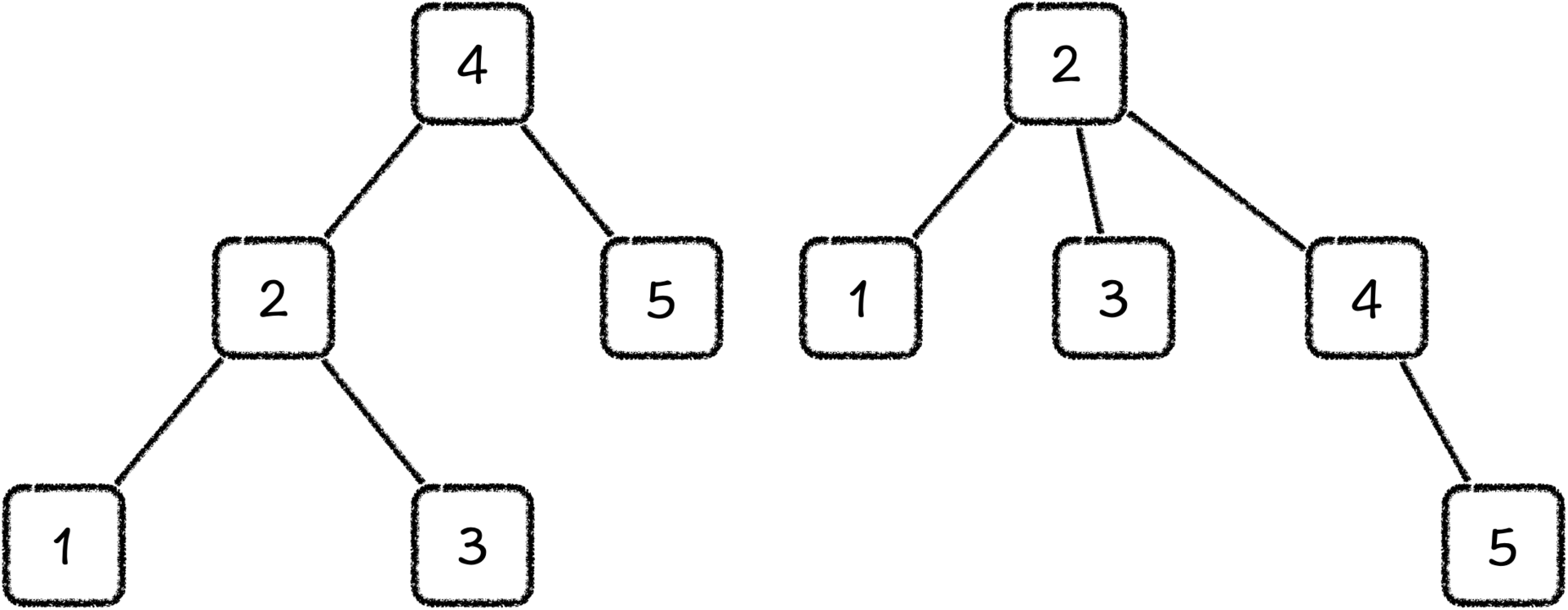
为了保持二叉树的性质,我们就需要选出一个孩子节点移动到另一个空位上。这个时候,1、3、5有两个空位,4有一个空位。我们可以把其中一个孩子节点移到5上吗?你千万不要被这个简单的例子迷惑了,5 号节点完全可以代表一棵左右孩子双全的子树。
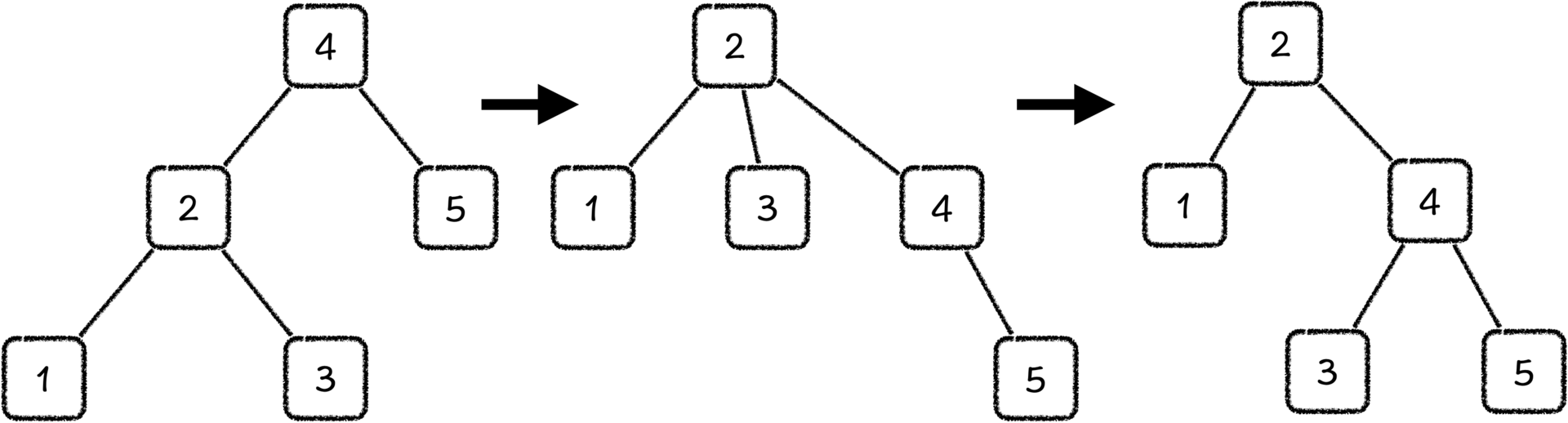
因此,我们需要找到唯一一个一定会出现一个空位的节点。没有错,就是原来的根节点,所以我们应该把2 号节点多出来的一个孩子节点放到原根节点,也就是4的下面。
相信你也看到了,根节点空出来的位置刚好是左孩子的位置,而新的根节点 2 号节点,由于它原本就是 4 号节点的左孩子,因此它的所有子树节点的值都小于 4 号节点。也就是说,2 号节点的任意一个孩子都可以放到 4 号节点的左孩子位置。
但是别忘了,我们还有一个目标,那就是保持原二叉树的中序遍历序列不变。如果我们把2号节点的左孩子变成了4号节点的左孩子,那在中序遍历之后,我们就无法先遍历到这些节点了,所以,我们只能把2号节点的右孩子,变成4号节点的左孩子。这也就保持了4号节点的中序前驱在新的树中,依旧是中序前驱。
Node *right_rotate(Node *root) {Node *temp = root->lchild;root->lchild = temp->rchild;temp->rchild = root;update_height(root);update_height(temp);return temp;}
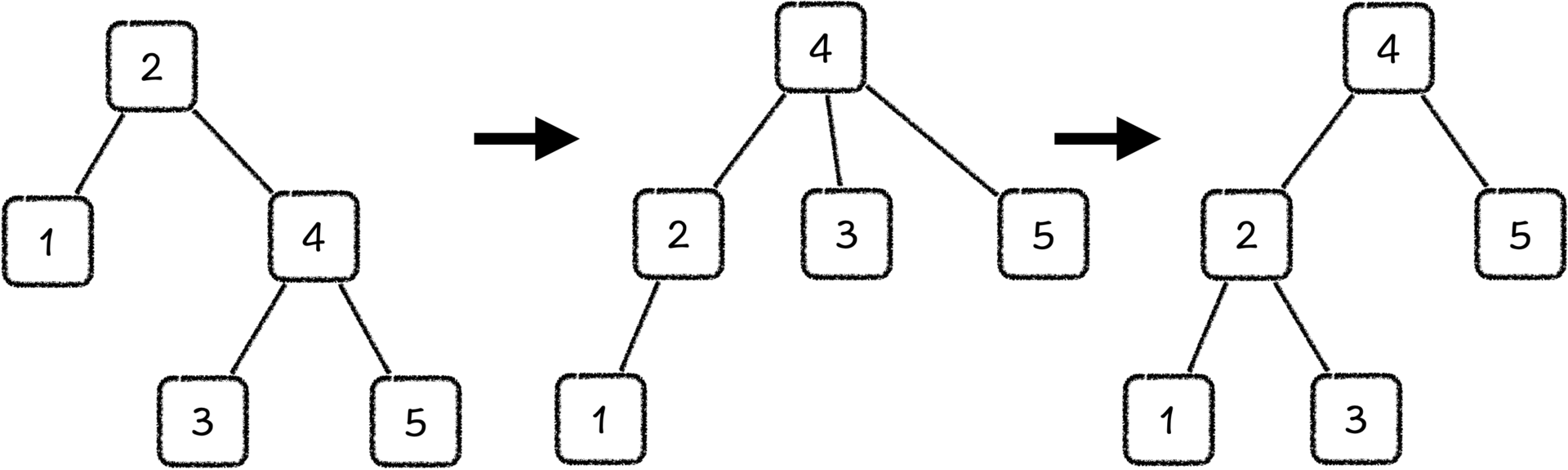
这种把二叉树的左孩子作为根进行的旋转操作,也被称作是右旋操作(Right Rotate),那与之对称的就是左旋操作(Left Rotate)。
Node *left_rotate(Node *root) {Node *temp = root->rchild;root->rchild = temp->lchild;temp->lchild = root;update_height(root);update_height(temp);return temp;}
看到这里,相信你也发现了,二叉树的旋转操作可以有效地改变左右两棵子树的树高差,所以,旋转操作是平衡树保持平衡的关键操作。接下来,我们就来聊一聊,平衡树是怎样利用旋转操作保持平衡的。
AVL树的基本操作
为了保持树的平衡,我们首先需要知道现在这棵树是不是平衡的。这里,我们可以直接计算平衡树的树高差,我们用右子树的树高减去左子树的树高,把得到的差叫做平衡因子。在平衡树中,平衡因子只可能有3个值:+1,-1和0,一旦某一个节点的平衡因子出现了这3个值之外的数值,就说明这棵子树需要调整。
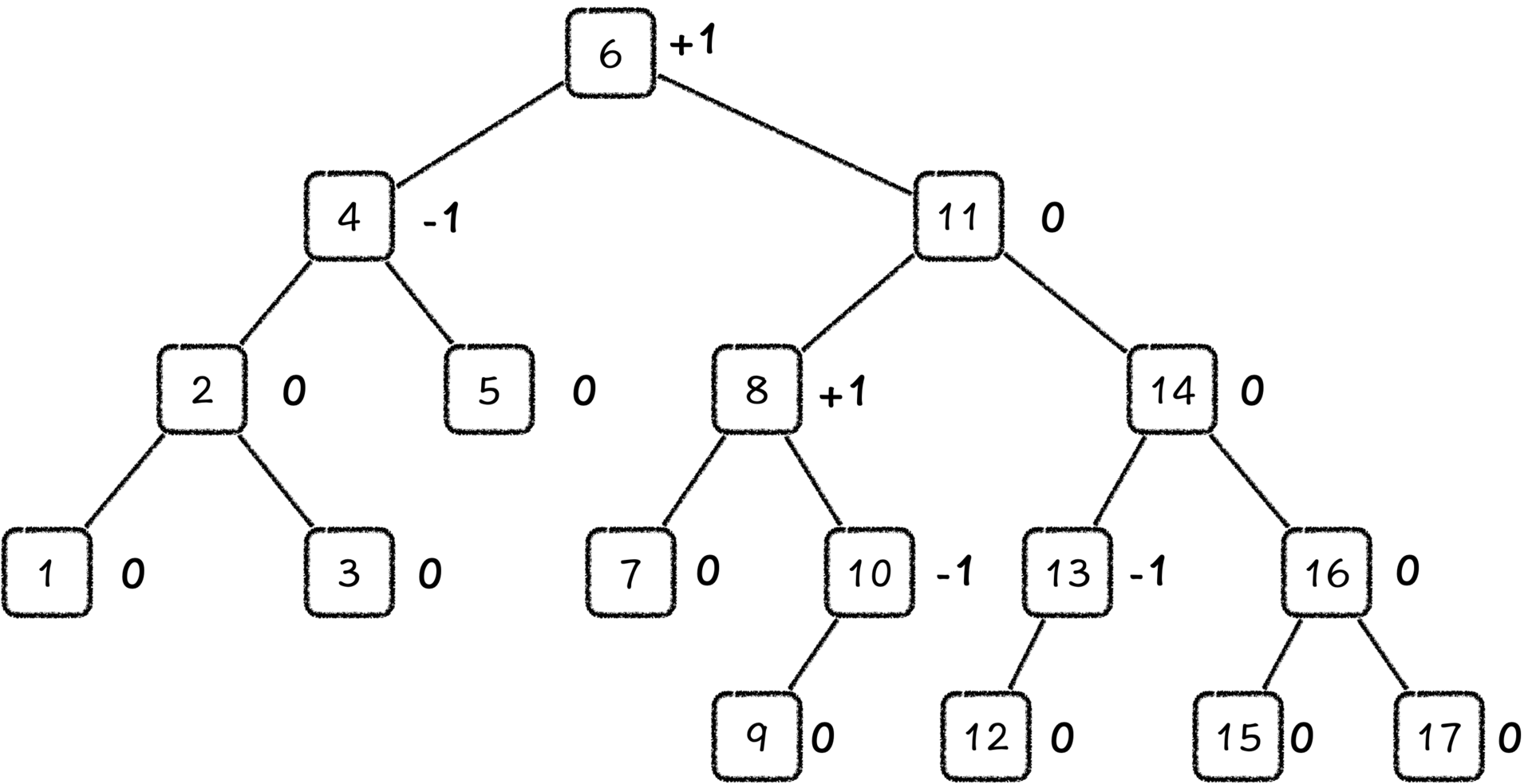
我们知道,旋转操作可以有效地改变左右两棵子树的高差,所以,我们也主要依赖旋转操作来调整平衡因子。那具体怎么做呢?我们可以结合平衡树的更新操作一起来学习。
//AVL树节点定义,需要增加数据域h记录当前节点树高#define H(root) (root)->h#define K(root) (root)->key#define L(root) (root)->lchild#define R(root) (root)->rchildtypedef struct Node {int key, h;struct Node *lchild, *rchild;} Node;
AVL树的插入
首先,是插入操作。我们先想两个问题,在向平衡树中插入节点的时候,树上会发生什么样的变化?我们怎么利用旋转操作让二叉排序树回归到平衡中呢?
因为影响平衡的主要因素是树高,所以我们主要考虑插入节点后对树高的影响就好啦。
最简单的情况,就是我们插入一个节点之后,并没有影响到子树的树高,这个时候,我们不需要进行调整。
第二种情况,我们插入一个节点之后,虽然影响到了子树的树高,但没有影响到子树平衡。这种情况其实还能细分成三种情况。第一种,我们把节点插入到根节点平衡因子为0的子树中的任意一处,第二种,我们把节点插入到根节点的平衡因子为+1的子树的左子树中,第三种,我们把节点插入到根节点的平衡因子为+1的子树的右子树中。这三种情况听起来可能有点绕,你可以结合任意一张示意图来理解。
所以,我们需要考虑的情况,只有插入了节点之后,确实影响到了树的平衡。其实,这种情况还能进行细分。下面,我就详细来说说。
首先,我们向一棵平衡因子为+1的子树的右子树中插入一个节点,这样右子树的会树高增加,这个节点的平衡因子就变成了+2。

我们看到,节点A的平衡因子超出了限制,所以我们需要降低A节点的平衡因子。那么这棵树只要经历一次左旋操作就能恢复平衡了。
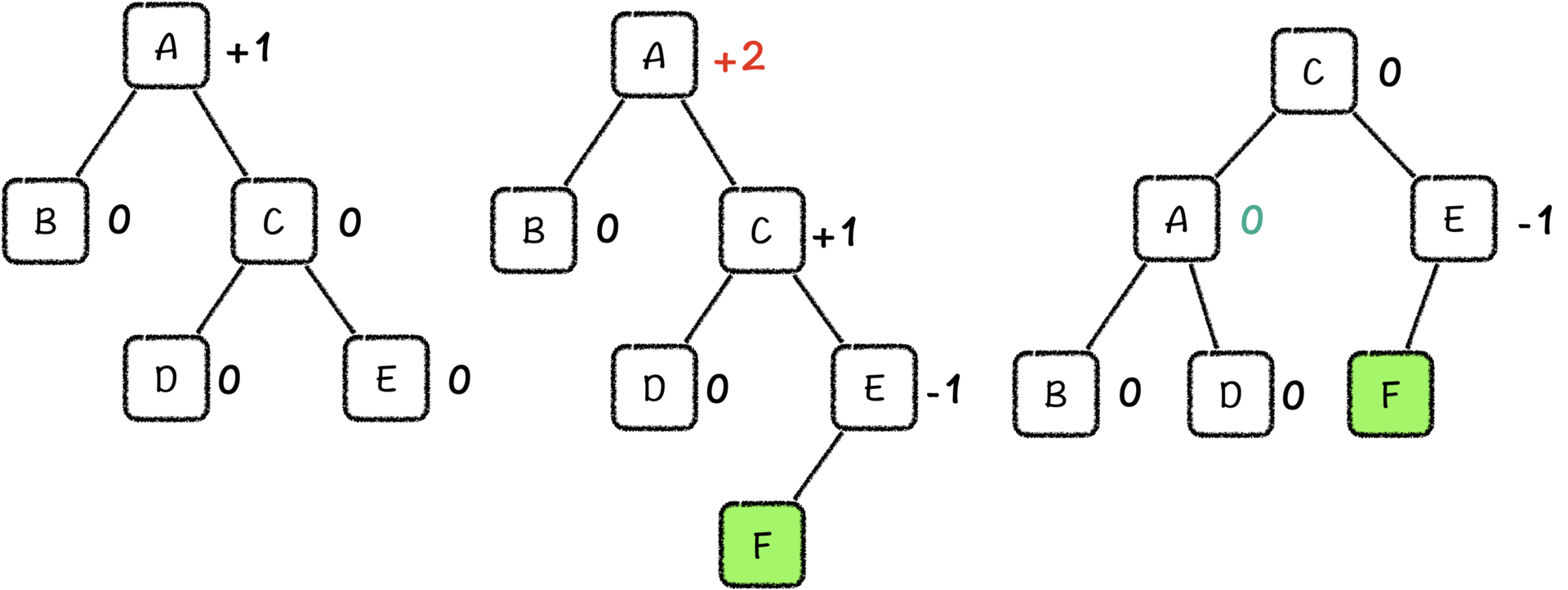
这种情况其实还有一种对称的情况:我们向平衡因子为-1的子树的左子树中插入节点,因为影响了左子树的树高,所以平衡因子就变成-2,怎么恢复平衡,相信我不说,你也知道了。
其实前面这些情况,都是向一个方向插入的节点。比如说,刚才我们插入的位置是子树A的最右子节点下面,这样A的右子树C的平衡因子就变成了+1。但是,还有一种情况是,我们插入了节点之后,C的平衡因子就变成了-1。

如果我们把这种情况直接做左旋处理的话,很显然,右子树C的左子树D就会直接成为A的右子树,那么左子树的树高则变成了3,右子树由于只有一个E节点,树高变成了1,根节点C的平衡因子变成了-2,树仍旧是不平衡的。这个时候,我们该怎么办呢?
我们最终还是要经过左旋让这棵树变平衡,所以我们只能想办法让树在左旋之后,左子树的树高不会增加那么多。因此,我们需要做的是,减少掉右子树C的左子树的树高。那由于C的平衡因子是-1,我们对C子树进行右旋,也不会影响该子树的平衡性,还可以让左子树的树高变成-1。
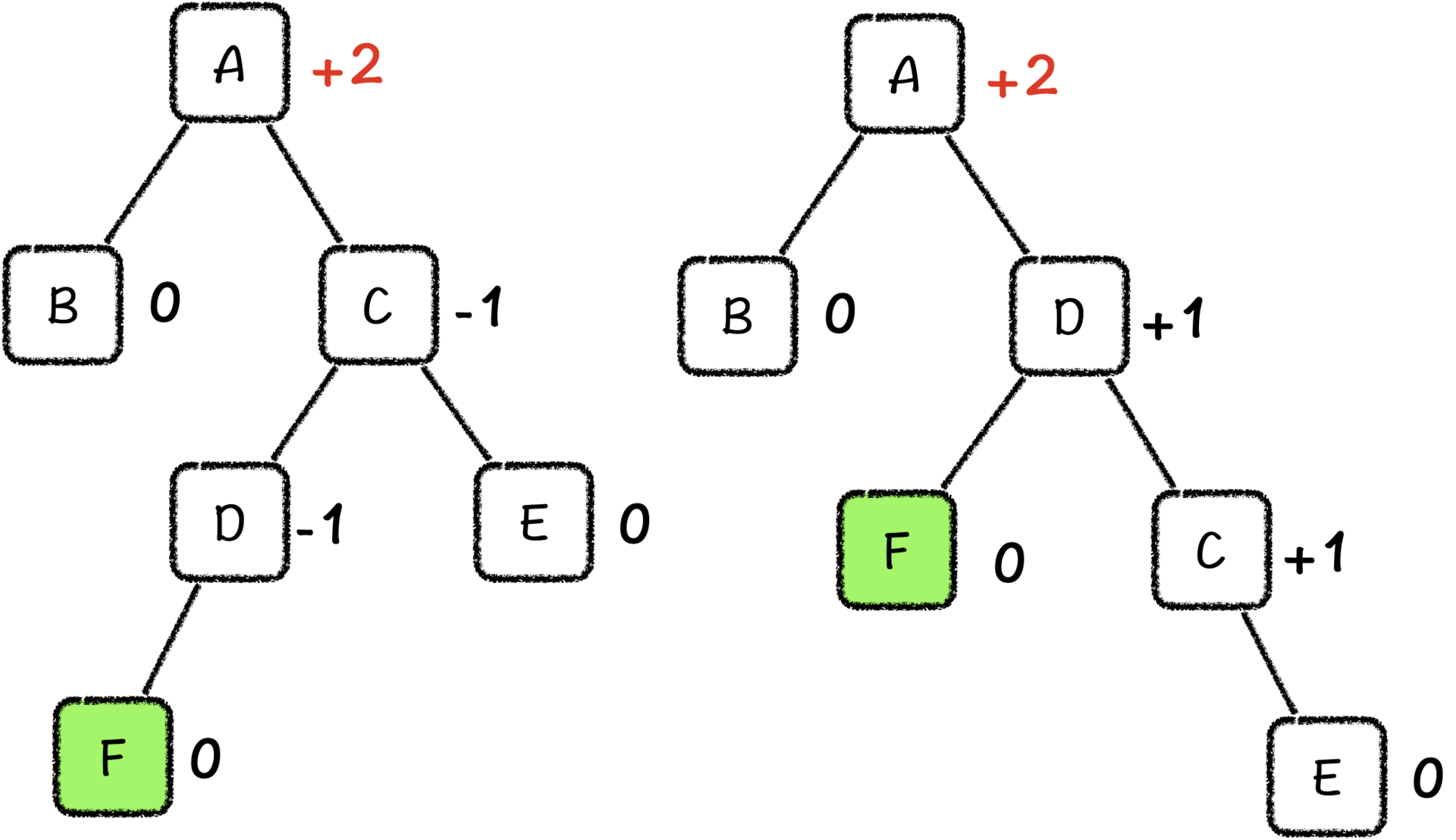
发现了吗,这种情况刚好又和第一种情况是一样的了,我们再进行一次左旋,就可以将这棵树重新调整到平衡状态了。
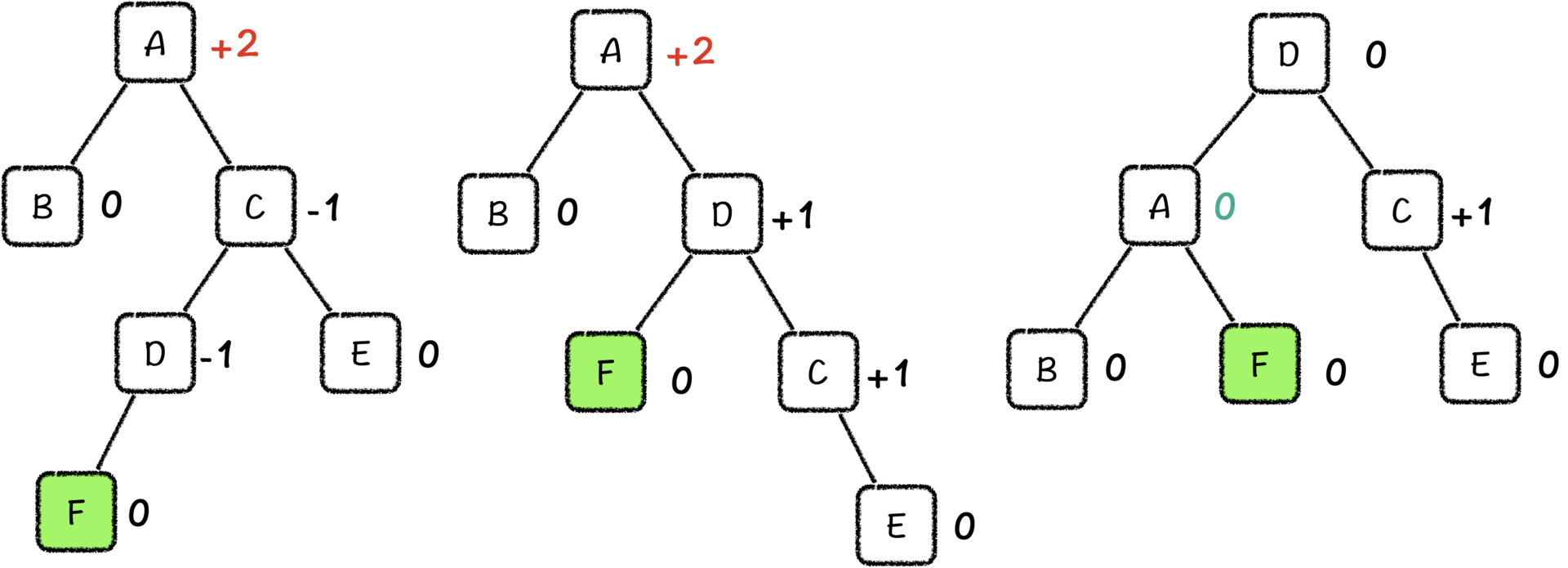
当然,这种情况也是有对称情况的,对称情况是什么,怎么解决,你可以自己操作试试。
说了这么多,这里我再带你做个总结。我们通过旋转操作来调整二叉树的平衡性的原则是,如果插入节点破坏了树的平衡,我们就需要找到这一次的插入操作,到底影响了哪一棵子树的树高,无非是左、右两种。
当我们向右子树中插入节点,导致树不平衡时,我们最终一定是通过左旋操作让树重归平衡。但如果我们插入节点的位置是右子树的左子树,那在左旋的时候,这棵左子树会被新的左子树继承,它不平衡的树高也会被继承,所以我们仍然是要通过一次额外的旋转,将不平衡的左子树解决掉。对称情况同理。
//AVL树调整平衡Node *maintain(Node *root) {if (abs(H(L(root)) - H(R(root))) <= 1) return root;if (H(L(root)) > H(R(root))) {if (H(R(L(root))) > H(L(L(root)))) {root->lchild = left_rotate(root->lchild);}root = right_rotate(root);} else {if (H(L(R(root))) > H(R(R(root)))) {root->rchild = right_rotate(root->rchild);}root = left_rotate(root);}return root;}
实际上,插入节点导致平衡树不平衡的情况,归根到底就是这两种,或它们的对称情况。所以在插入节点的过程中,我们只需要利用这两种处理方式,就可以一直让树保持平衡状态,这也就保证了这棵树的树高最小,每次插入索引的时间复杂度都是$O(log_2N)$。
除了插入节点会导致树不平衡,平衡树的插入操作的其他部分就和一般二叉排序树是一样的了,相信你也能理解,我就不多说了。
当然,平衡树的删除操作也是类似的,在删除了一个节点之后,我们也要解决树不平衡的问题。那除此之外,它的删除操作也和二叉排序树的删除操作一样。
AVL 树的级联合并
在解决了平衡树的基本操作之后,我们来讨论一个更加有挑战性的问题。怎么把两棵平衡树合并成一棵平衡树,并且我们假设,一棵树中的所有值都比另一棵树大。
首先,最直观合并方法,就是把其中一棵平衡树的N个节点逐一插入到另一棵带有M个节点的平衡树中,那么合并的时间复杂度就是$O(Nlog_2M)$。这种合并的代价看上去也可以接受。
但是,我们还有一种更加巧妙的方法,就是利用有序序列的边界信息。
假设,我们要合并的两棵树分别是$T_1$和$T_2$,并且,这两棵树的值之间的关系是$max(T_1)<min(T_2)$,这两棵树之间高度的关系是$height(T_1)\ge height(T_2)$。
第一步,我们要找到$T_2$中最小的节点J,把它删除,得到树$T_2’$,那$T_2$中剩余的节点就全都在J的右子树之中了。
第二步,我们在$T_1$中,不断向右下走,找到一棵子树P,让$height§-height(T_2’)=0或1$。
由于$T_1$中的值都比$T_2$中的值小,我们就可以推出,J的值一定比P的值大,因此我们就把P当作J的左子树,$T_2$剩余的节点当作J的右子树,再把P的父亲当作J的父亲。
因为P是向右下寻找得到的,所以$T_1$中剩余的值依旧符合二叉排序树的性质。而由于我们控制了节点P所在的高度,因此,这个问题我们可以看作是把J节点插入到了$T_1$中。对称情况的解决方法也是类似的。
课程小结
平衡树的内容讲完了,我们一起来做个总结。
这节课,我们先学习了二叉排序树上,一种非常基础也非常重要的操作,二叉树的旋转操作。旋转操作,分成左旋操作和右旋操作,它们都能有效改变树高,所以利用旋转操作,我们可以时刻保持平衡树是平衡状态的。这也让我们在平衡树上的查找,变得非常地容易。
接着,我们又一起讨论了平衡树的合并和分解操作。其实核心原则就是在插入和删除节点之后,如果树不平衡了,我就进行左旋或者右旋操作,让它恢复平衡。这让我们可以更加灵活地操纵有序序列。
不过,即使平衡树在索引上保持了如此优秀的效率,但为了能让树在频繁更新的时候依然保持平衡,我们仍旧要付出相当大的代价。
因此,在实际的应用中,我们很可能不需要让树时刻保持严格的平衡,而只需要让树保持一个相对平衡的状态就行了,当树的不平衡程度打破了我们的忍耐限度时,再让树通过少量的调整恢复到相对平衡的状态中。这种二叉排序树也被称作近似平衡二叉排序树,它可以应用于需要频繁更新的结构上。
那在接下来的课程中,我会带你学习一种应用非常广泛的近似平衡二叉树,也就是红黑树。
课后练习
今天,我们在讨论平衡树中插入或者删除元素的时候,还有一些对称情况没有细说。你能结合你的理解,把这些对称情况的算法实现出来吗?
欢迎在留言区分享你的答案,也希望你能把这节课的内容转发出去。那今天就到这里了,我是胡光,我们下节课见!