02 | 快排优化:举一反三,轻松面对快排面试题
你好,我是胡光,欢迎回来。今天我们来聊聊快排算法的升级。
我们知道,用快速排序算法在一堆无序的数字中查找第k位元素,需要先对原数字序列快速排序以后,才能输出第k位元素。这样整体的时间复杂度,如果控制得好的话,可以达到 $O(nlogn)$,但是这个方法存在2个问题。
首先,我们是想求排名第 k 位的元素,又不是真的想对整体序列进行排序。如果对全部数学序列进行快排,我们实际上做了大量的无用操作,这会导致算法效率很低。其次,快速排序算法的时间复杂度不稳定,很有可能退化到最坏的时间复杂度$O(n^2)$。
那有没有不需要排序,且效率更高的做法呢?或者,就算依然要使用快速排序算法,我们要如何才能让它的时间复杂度大概率稳定在$O(nlogn)$呢?
今天,我们就带着这两个问题,来继续查找第k位的元素。
针对第一个问题,我们可以使用快速选择算法解决。快速选择算法是基于快速排序算法的一种拓展算法,它可以在不对数据整体进行排序的前提下,快速找到排名第 k 位的元素,而且时间复杂度还能优化到 $O(n)$。而对于第二个问题,我会给你讲几种快速排序中的优化方法。这些优化方法,会使你应对快速排序相关的面试题的时候,更加游刃有余。
理解快速选择算法的核心原理
首先,我们来看快速选择算法。快速选择算法的基本思想是,当我们需要快速找到一个元素 X,并且使得小于 X 的元素数量是 k-1 个时,那 X 就是我们要查找的排名第 k 位的元素了。
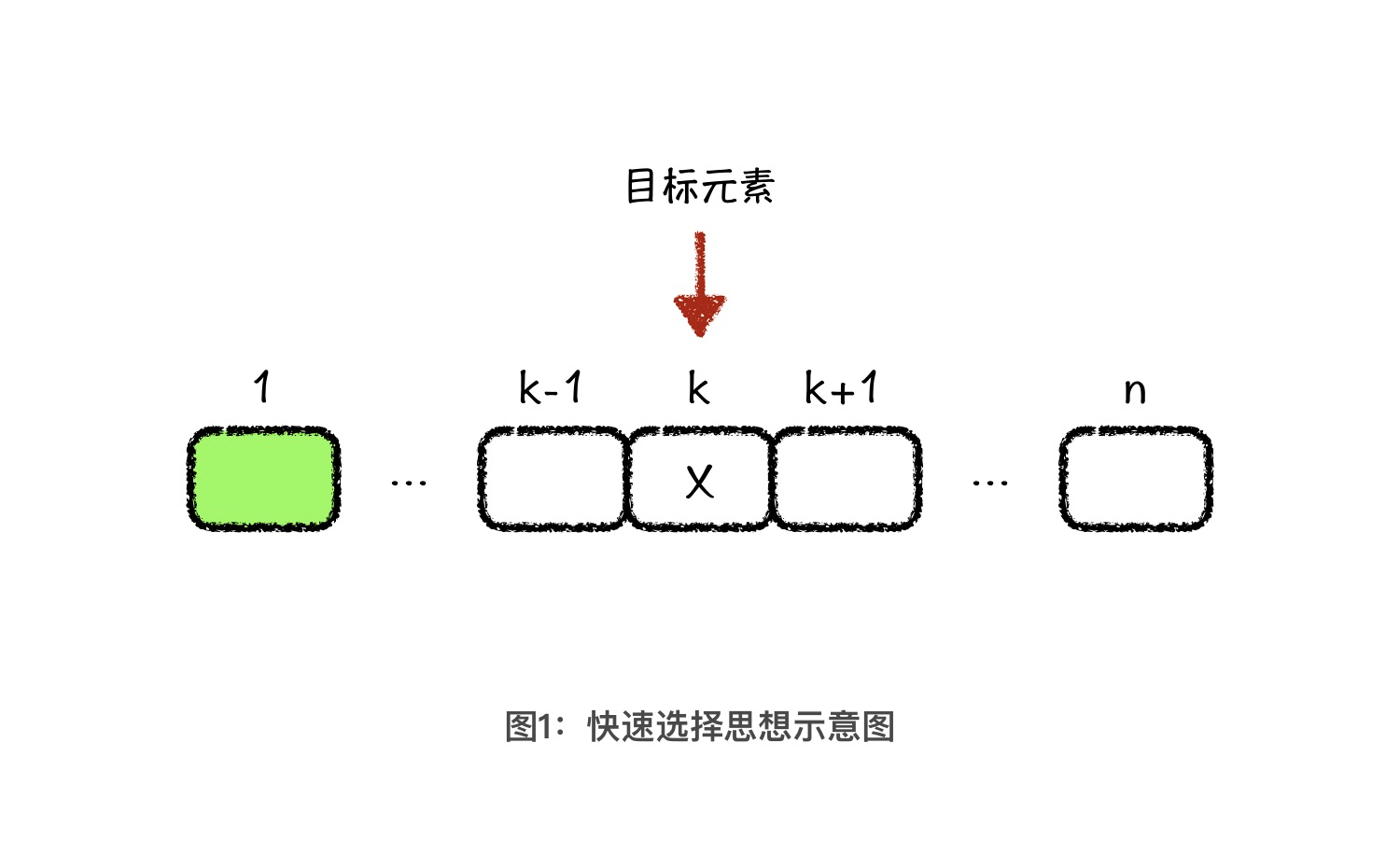
这也就意味着,我们没必要对原数组进行整体排序,只需要找到满足上面我们所说条件的元素 $X$ 即可。这一点你有没有觉得很熟悉?没错,这和 partition 过程很像。partition 过程就是在每一轮排序中找到一个基准值元素的正确位置 ind ,并且它最厉害的地方在于,它会用基准值将数组分成前后两部分,小于等于基准值的元素在前面,大于等于基准值的元素在后面。
那我们是不是可以用 partition 过程实现快速选择呢?接下来,让我们先来分析一轮 partition 过后,基准值元素的排名 ind 与 k 之间的关系。我把可能出现的三种情况都列了出来:
- 如果 ind 正好等于 k,那说明当前的基准值,就是我们要找的排名第 k 位的元素;
- 如果 ind 大于 k,说明排名第 k 位的元素在基准值的前面。接下来,我们要解决的问题就是,在基准值的前面查找排名第 k 位的元素;
- 如果 ind 小于 k ,就说明排名第 k 位的元素在基准值的后面,并且,当前包括基准值在内的 ind 个元素,都是小于基准值的元素。那么,问题就转化成了,在基准值的后面查找排名第 k - ind 位的元素。
这么说你可能还不是特别理解,下面,我们再结合下面的示意图理解一下。假设本轮基准值为 X,绿色区域中的值均小于 X,蓝色区域中的值都大于 X,基准值的位置是 ind。当 k < ind 时,下一轮我们就在绿色区域中继续查找,当 k > ind 时,下一轮我们就在蓝色区域中继续查找。这个过程,其实有点儿类似于二分查找的思想。
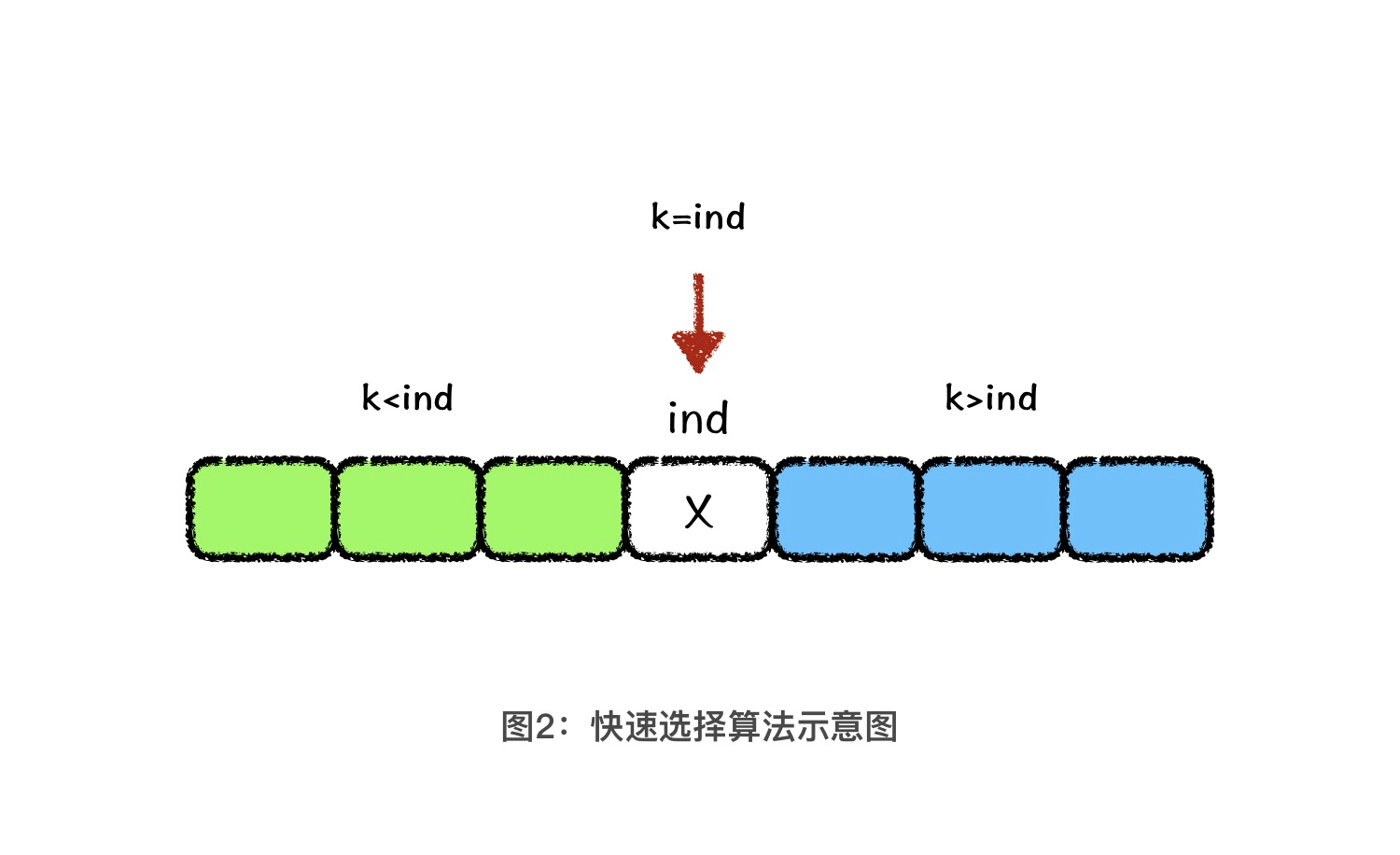
也就是说,经过一轮 partition 操作以后,我们总能将在当前数组中查找排名第 k 位元素的问题,转化成递归子问题。也就是在基准值的前面查找排名第 k 位的元素,或者在基准值的后面查找排名第 k - ind 位的元素。
那快速选择算法的时间复杂度究竟是多少呢?分析起来很简单,你可以自己试试。为了便于你验证自己的分析结果,先给你个结论:快速选择算法的时间复杂度,最好情况是 $O(n)$ ,最坏情况是 $O(n^2) $,平均情况是 $O(n)$ 。并且,为了让快速选择算法能够发挥得更稳定,我们需要在选择基准值的时候做一些优化。具体优化方法,你可以参考快排优化中的基准值选择优化,我们马上就会讲到了。
三种快排优化
以前我在做面试官的时候,当问到面试者会不会快速排序,他们都会回答:会。但如果我让他们说一下快速排序的内容,80% 的面试者都只能说出快速排序的基础知识,也就是我们上节课讲过的内容,只有 20% 的人能说出快排的优化内容。当然了,能说出这20%内容的人面试分数就会相对更高。
那么为了让你对快排的理解更加深刻,也在面试的时候能多一些“谈资”,我会给你讲三个比较常见的快排优化,分别是单边递归优化、基准值选取优化和partition 操作优化。
优化一:单边递归优化
第一个优化被形象地称为:单边递归优化。这是什么意思呢?
我们知道,在快排函数的实现过程中,当本层完成了 partition 操作以后,剩余的工作就是等待着左边和右边的排序完成。代码如下所示:
quick_sort(arr, l, x - 1); // 对左半边排序quick_sort(arr, x + 1 , r); // 对右半边排序
这段代码就分别对基准值的左右两边进行了排序的递归调用。从程序的运行时间来考虑的话,我们每次函数调用,都会消耗掉一部分运行时间。那只要我们可以减少函数调用的次数,其实就可以加快一点程序运行的速度。
因此,单边递归优化的方式,就是当本层完成了 partition 操作以后,让本层继续完成基准值左边的 partition 操作,而基准值右边的排序工作交给下一层递归函数去处理。
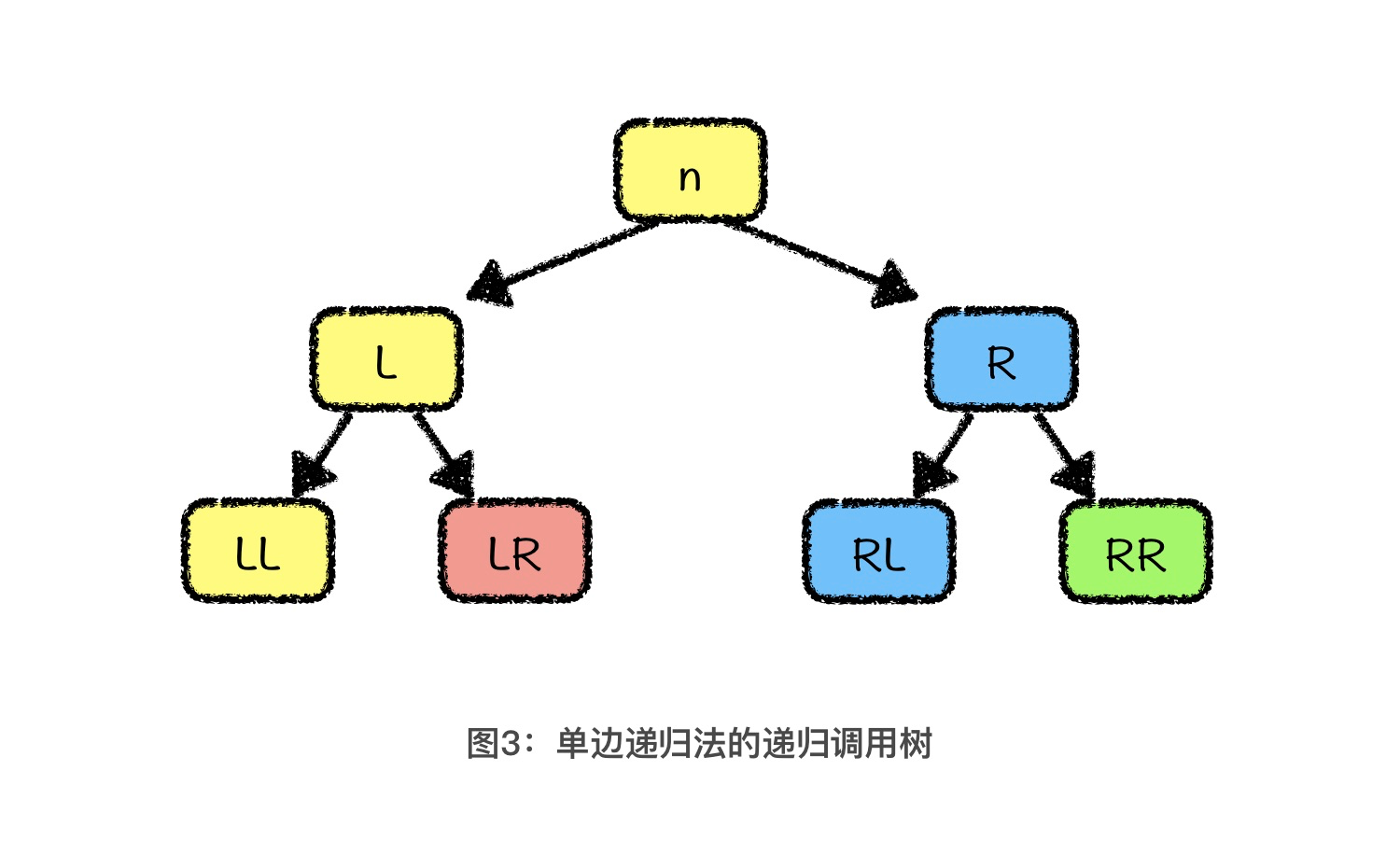
经过单边递归优化后生成的递归树如上图所示,为了方便你理解,我把在同一个函数调用内的操作用同样的颜色表示。一共用了黄色、红色、蓝色、绿色这4种颜色,也就是说我们实际调用了4次函数。而如果不采用单边递归法,实际发生的函数调用次数就是图中二叉树的节点个数,也就是7次。可见,我们采用了单边递归法以后,函数实际调用次数减少了一半。
下面是一段单边递归法的代码:
void quick_sort(int *arr, int l, int r) {while (l < r) {// 进行一轮 partition 操作// 获得基准值的位置int ind = partition(arr, l, r);// 右侧正常调用递归函数quick_sort(arr, ind + 1, r);// 用本层处理左侧的排序r = ind - 1;}return ;}
从代码中可知,l 和 r 是数组中待排序的区间范围,ind 是本轮 partition 操作后基准值的位置。当找到基准值的位置以后,对于右侧从 ind + 1 到 r 位置,我们就正常调用递归函数。然后,我们通过将 r 设置为 ind - 1,直接利用本层 while 循环逻辑,继续对左侧进行 partition 等相关排序操作。
优化二:基准值选取优化
说完了单边递归,我们接着来说快排中对于基准值选取的优化。我们知道,如果基准值选取不合理的话,快速排序的时间复杂度有可能达到 $O(n^2)$ 这个量级,也就是退化成和选择排序、插入排序等算法一样的时间复杂度。只有当基准值每次都能将排序区间中的数据平分时,时间复杂度才是最好情况下的 $O(nlogn)$。
当然,我们没有办法在一个无序数组中,用 $O(1)$的时间复杂度找到一个可以将数组平分的基准值。退而求其次,我们能不能尽可能地找到一个可以大概率将数组平分的数字呢?这就是接下来我要给你讲的,关于基准值选取的一个优化策略,三点取中法。
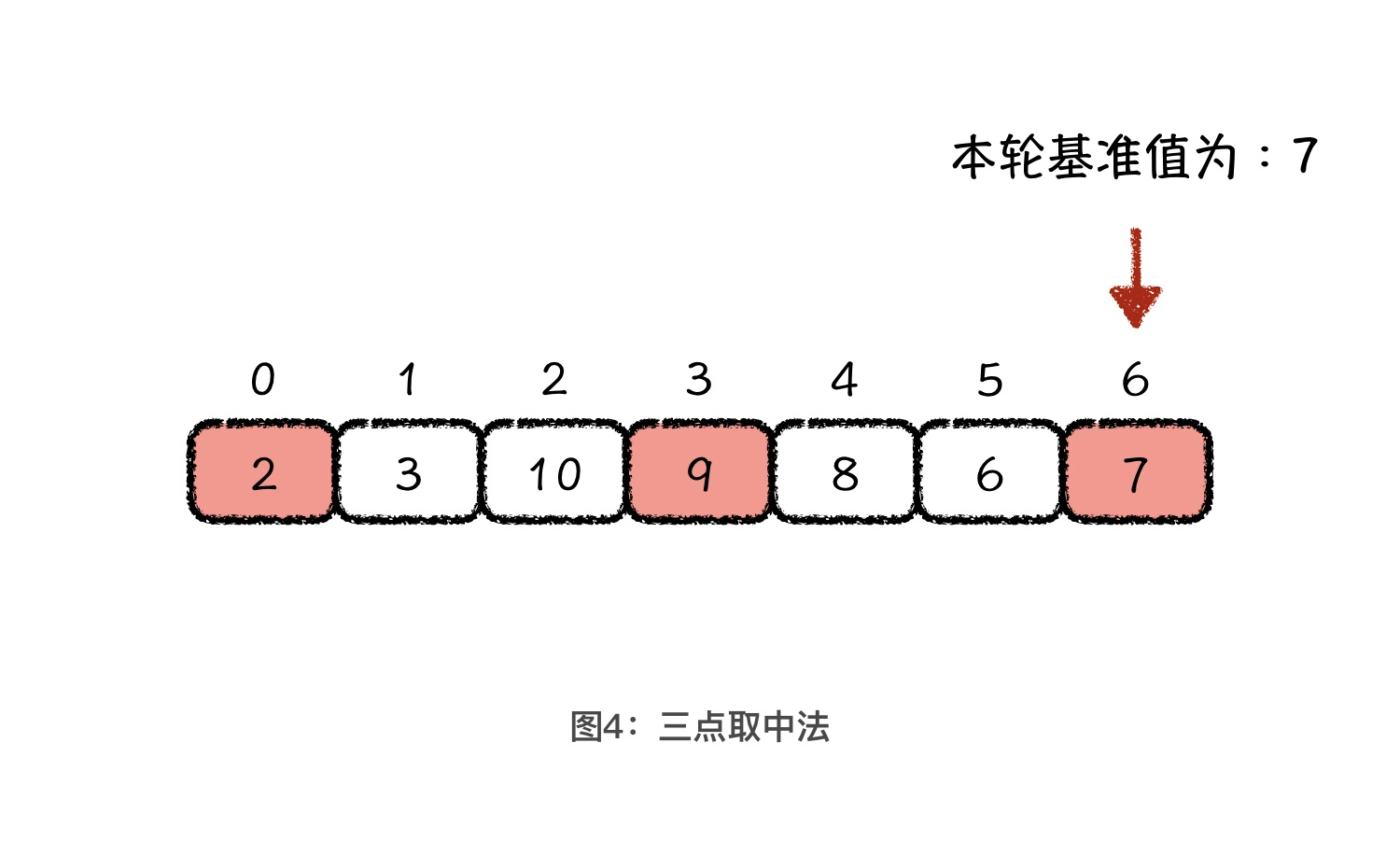
所谓三点取中法,就是每一轮取排序区间的头、尾和中间元素这三个值,然后把它们排序以后的中间值作为本轮的基准值。当然,你也可以根据自己的理解,调整要选取的这三个值的位置。我们就以上图为例,假设本轮的三个值分别为2、9、7,中间值是7,所以,本轮的基准值就是 7。
在实际应用中,由于基准值选择不合理而陷入最差情况的概率,我们利用三点取中法就已经可以大幅度降低了。而且,这种方法实现起来也比较简单,所以 C++ STL 中的 sort 实现,其实就是采用的这种基准值选择优化策略。
优化三:partition 操作优化
前面我们讲的两种优化方法,分别是从递归代码结构和基准值选取这两方面对快速排序做了优化。下面,我再给你讲一种对 partition 代码实现过程进行优化的方法。这种优化方法很容易被我们忽略。那它到底是怎么优化的呢?
在说它之前,我们先来回顾一下 partition 的实现过程:先从后向前找个小于基准值的数字放到前面,再从前向后找个大于基准值的数字放到后面,直到首尾指针相遇为止。其实,想要比较容易地理解这个过程,我们可以假设基准值的位置是数组中间的一条分割线,小于基准值的都是绿色元素,大于基准值的都是红色元素。如下图所示:
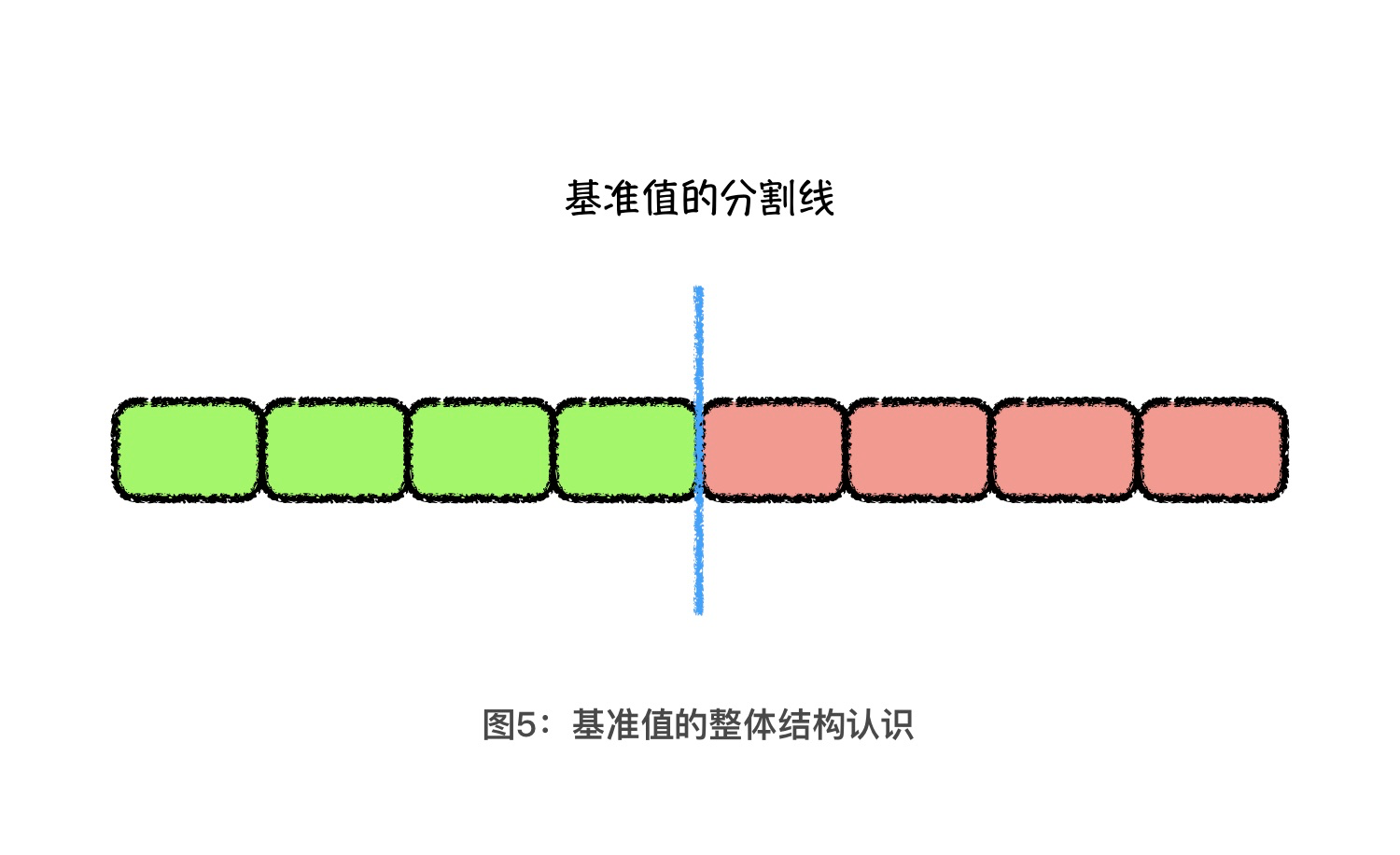
这个时候,你可以想一想,在什么情况下,我们才需要将基准值后面的元素调换到前面?一定是因为这个分割线后面有绿色的元素。而且,基准值的客观位置不变,红色与绿色元素数量是确定的,所以存在多少个绿色元素在基准值位置的后面,就一定存在多少个红色元素在基准值位置的前面。
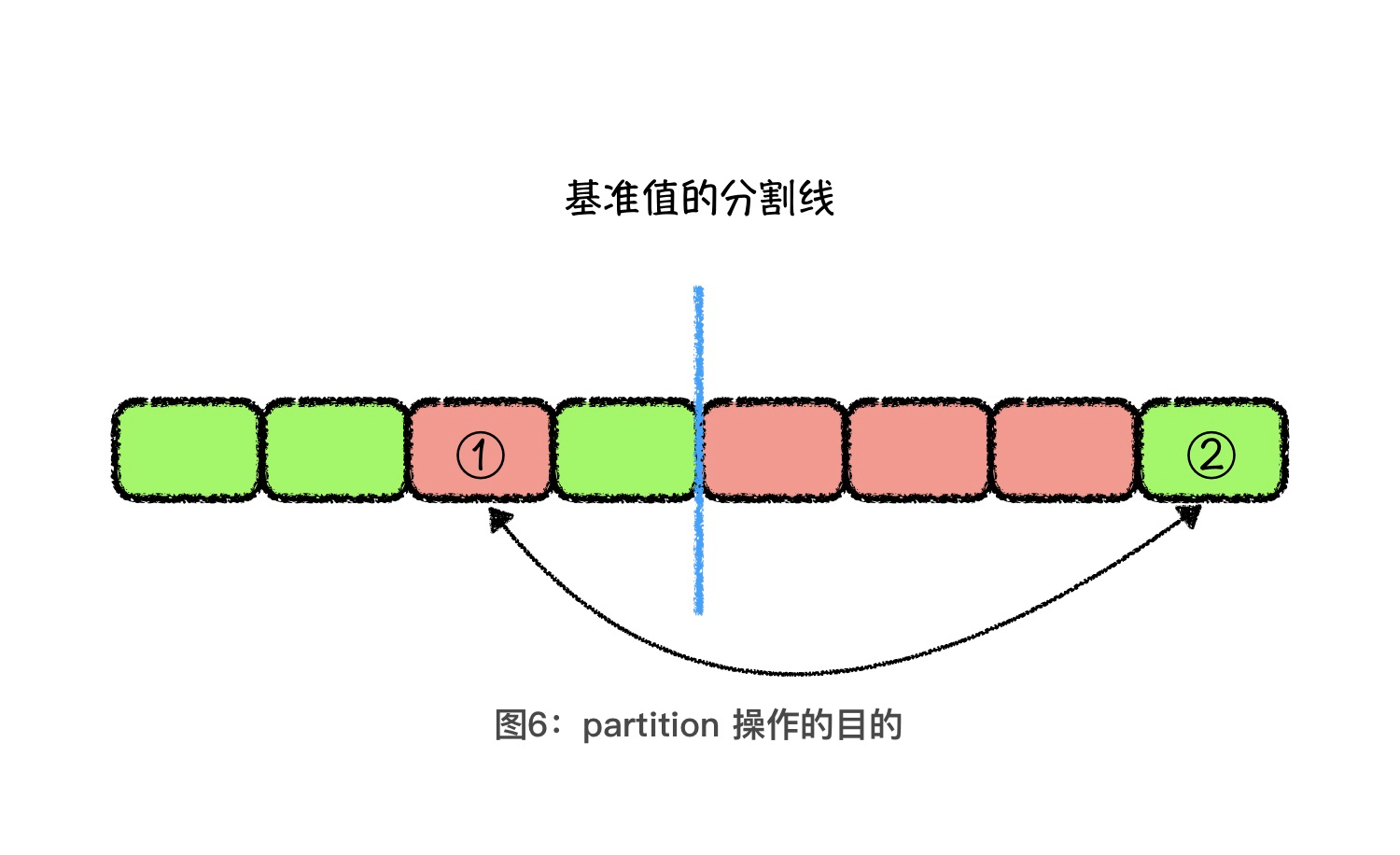
那 partition 操作的目的,就是要把基准值位置后面的绿色元素调整到前面,将基准值位置前面的红色元素调整到后面。也就是交换上图中 1、2 号元素的位置。既然需要调换的红色与绿色元素的数量相同,我们就可以让头指针向后查找红色元素,尾指针向前查找绿色元素,然后交换头尾指针所指向的元素,重复这个过程,直到头尾指针交错后停止。这就是对partition 操作进行的优化。
课程小结
这节课,我们讲了快速选择算法,和针对快速排序算法的三种优化。这里,我希望你能记住4件事情:
- 快速选择算法可以用来快速查找一个序列中排名第 k 位的元素;
- 单边递归法可以使快排过程中的递归调用次数减少一半,并且,这种优化方法也可以使用在所有和快速排序类似的程序结构中;
- 三点取中法能帮助我们选出更加合理的基准值,保证快速排序的运行效率;
- 优化 partition 的操作,通过减少程序实现中的比较操作,来提高程序的运行效率。
其中,关于快速排序的三种优化方法中,第二种优化,是为了使快速排序的时间复杂度尽量稳定在 $O(nlogn)$ 而提出来的,而第一种和第三种优化,没有对时间复杂度做优化,而是对程序的实际运行时间做了优化。对于实际工作而言,往往第一种和第三种优化,对我们的启发会更大一些。毕竟,公司内部的一个成型的技术或者产品中,能让你优化时间复杂度的部分可太少了。大多数时候我们能做的,就是切实可行地让系统运行得更快一些。
另外,我还要补充一点。在使用快速选择算法求解排名第 k 位的元素的过程中,其实当我们通过快速选择算法求得了第 k 位的元素值之后,再加上第 k 位元素值之前的元素,其实就找到了前 k 位的元素值。换句话说,快速选择算法不仅可以用于求解第 k 位的元素,也可以用于求解前 k 小或者前 k 大元素等问题,也就是所谓的 Top-K 问题。
如果你要参加面试,Top-K 问题也是经常被问到的一类问题。之后遇到具体问题的时候,我会详细来讲。
课后练习
请你参考partition 方法的优化代码,想想为什么这样的 partition 实现方法会比我们上节课实现的 parition 方法更优化。这里我给你个提示,这个新的 partition 实现方法,比旧的 partition 方法做了更少的比较操作,那具体少了多少呢?请你分析以后,把思考结果留在评论区中吧!
你知道快速选择算法的时间复杂度是怎么得到的吗?你可以借助上节课我们讲的二叉树的方法来试着分析一下。
好了,今天就到这里了。如果你的朋友也正在为快排优化的问题而头疼,那就快把这篇文章分享给他吧!我是胡光,我们下节课见!