17 | 红黑树（下）：红黑树的双黑节点与删除调整

你好，我是胡光。

上节课，我们讲了红黑树的5条基础性质，以及红黑树的插入操作。这节课我们依然围绕红黑树的5条性质，来讲讲红黑树的删除操作。

我们先来回顾一下红黑树的5条性质：

• 红黑树中每一个节点的颜色不是红色就是黑色；
• 红黑树的根节点都是黑色的；
• 每一个叶子节点都是黑色的；
• 如果一个节点是红色的，那它的两个孩子都是黑色的；
• 对于每一个节点，从它出发到它的后代叶子节点的所有简单路径上，黑色节点的数量都是相同的。

我们知道，向红黑树中插入一个新节点的时候，无论这个节点是红色还是黑色，都会破坏掉红黑树中的某几个性质，这就需要我们重新调整节点的颜色或者通过旋转操作来调整树的结构。那如果我们删除掉红黑树中的一个节点会造成什么样的影响呢？

红黑树中的双黑节点是什么？

首先，红黑树也是一棵二叉排序树，所以红黑树上的删除过程也和二叉排序树的删除过程类似。我们先来回顾一下二叉排序树的删除过程，假设我们要删除的节点是z，如果z没有孩子，直接删除就行，否则我们就得找到z的中序遍历前驱或后继顶替它的位置。

不过，因为红黑树的每一个节点都带有颜色信息，所以我们的每一次删除操作之后，还要保持红黑树的性质。具体怎么做呢？我们还是要分情况来讨论，逐个击破。

第一种情况，如果被删除的节点z有两个孩子，那我们需要找到的补位节点就是它的前驱节点或者后继节点y，将y补到z的位置之后，我们再把y的唯一一个孩子x补到y的位置。同时，我们还要把y的颜色替换成为z的颜色。这样，至少在z的位置上，颜色是没有改变的。

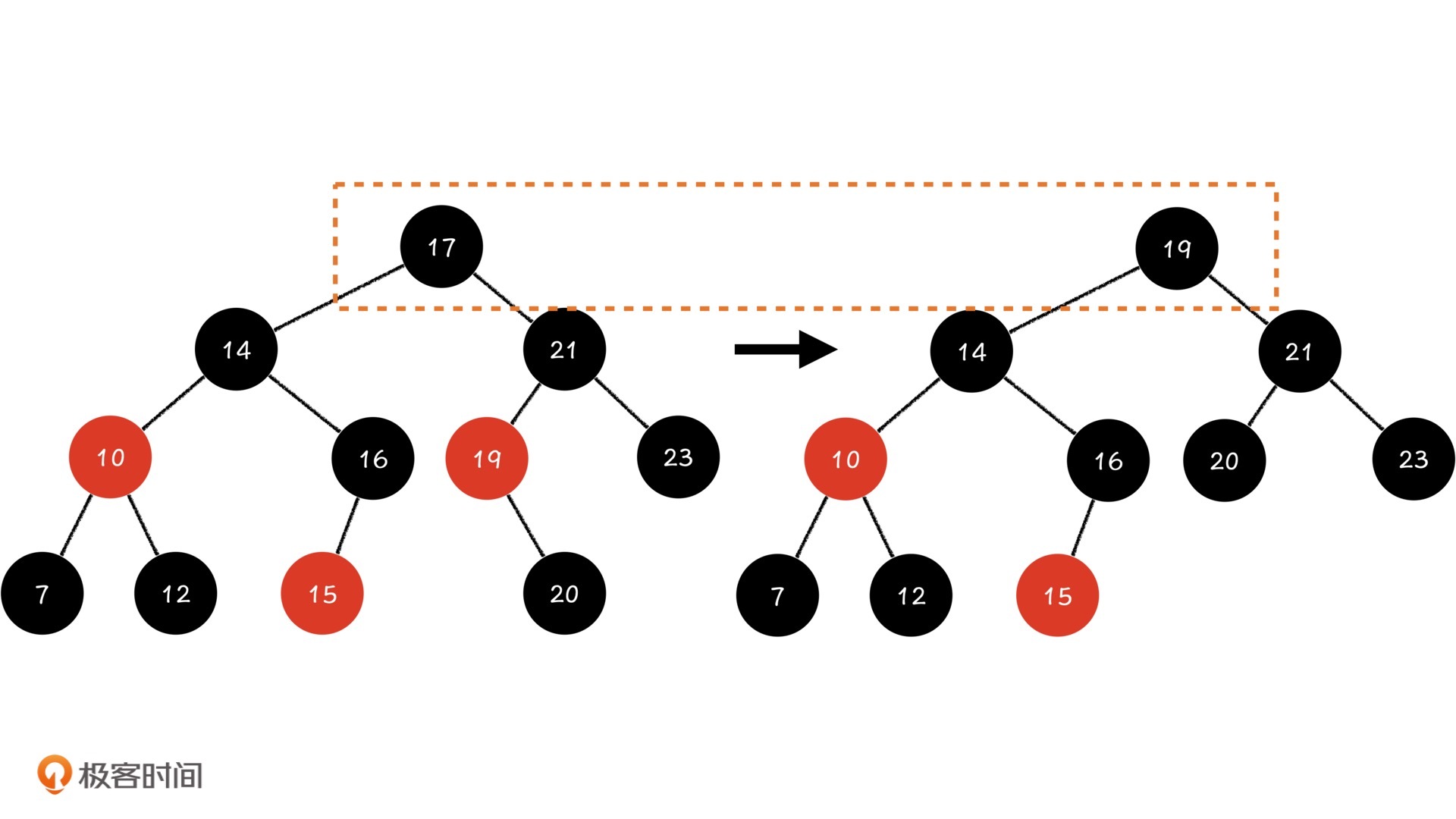
我们在以上图为例详细解释一下，如果想要删掉有两个孩子的节点17，我们只能向下寻找，把17的中序遍历后继19补到17的位置上，再把19染成黑色。这样节点17所在的局部位置，相当于没有发生任何变化，而实际受影响的，是节点17的后缀19节点的位置。因为19节点只有20这一个孩子节点，所以图中我们的实际操作就是删除掉节点19，将节点20补位到19的位置上。

总的来说，被删除的节点z有两个孩子这种情况非常简单，调整操作就相当于我们删除了z的后继节点y，然后用y唯一的孩子进行补位。所以我们重点要讨论的情况，其实是被删除的节点z只有一个孩子x。

我们先来想一个问题，如果被删除的节点是红色的，这对红黑树的性质有什么影响？答案是没有任何影响，因为在红黑树的5条性质中，我们只对黑色节点进行了明确的数量限制。那如果被删除的节点z是黑色的，这对红黑树的性质又有什么影响？这里，我们要结合它的孩子节点x的颜色来一起考虑。

首先，如果x是红色的，其实也不会对红黑树的性质有什么太大影响，我们只需要把x染成黑色就可以了。这是为什么呢？因为对于以z为根节点的子树来讲，虽然我们删了一个黑色的节点，让它每条路径上的黑色节点数都少了一个，但我们将红色节点染成黑色节点之后，它的黑色节点数量又恢复了。

可是，如果被删除节点z是黑色的，同时它的孩子节点x也是黑色的，那我们就无法补上这个丢失的黑色节点了。不过这也没关系，我们可以让这个补位的x节点暂时承担两份黑色节点的工作，这种节点我们叫它双黑节点（Doubly Black）或者双重黑节点，它虽然是黑色的，但我们认为它比单纯的黑色要黑很多，所以这个节点的存在打破了红黑树的性质1。

那遇到了这种节点之后，我们该怎么解决它呢？其实，整个红黑树的删除过程，我们都在围绕着如何解决双黑节点进行。想要消解掉双黑节点上的一个黑色节点，我们就必须要考虑消解掉它兄弟节点的一个黑色节点，这样才能保证以它的父亲为根的子树还是一棵合法的红黑树。因此，我们一共可以分4种情况来讨论。

Case 1：x的兄弟节点w是黑色节点，w的两个儿子都是黑色节点

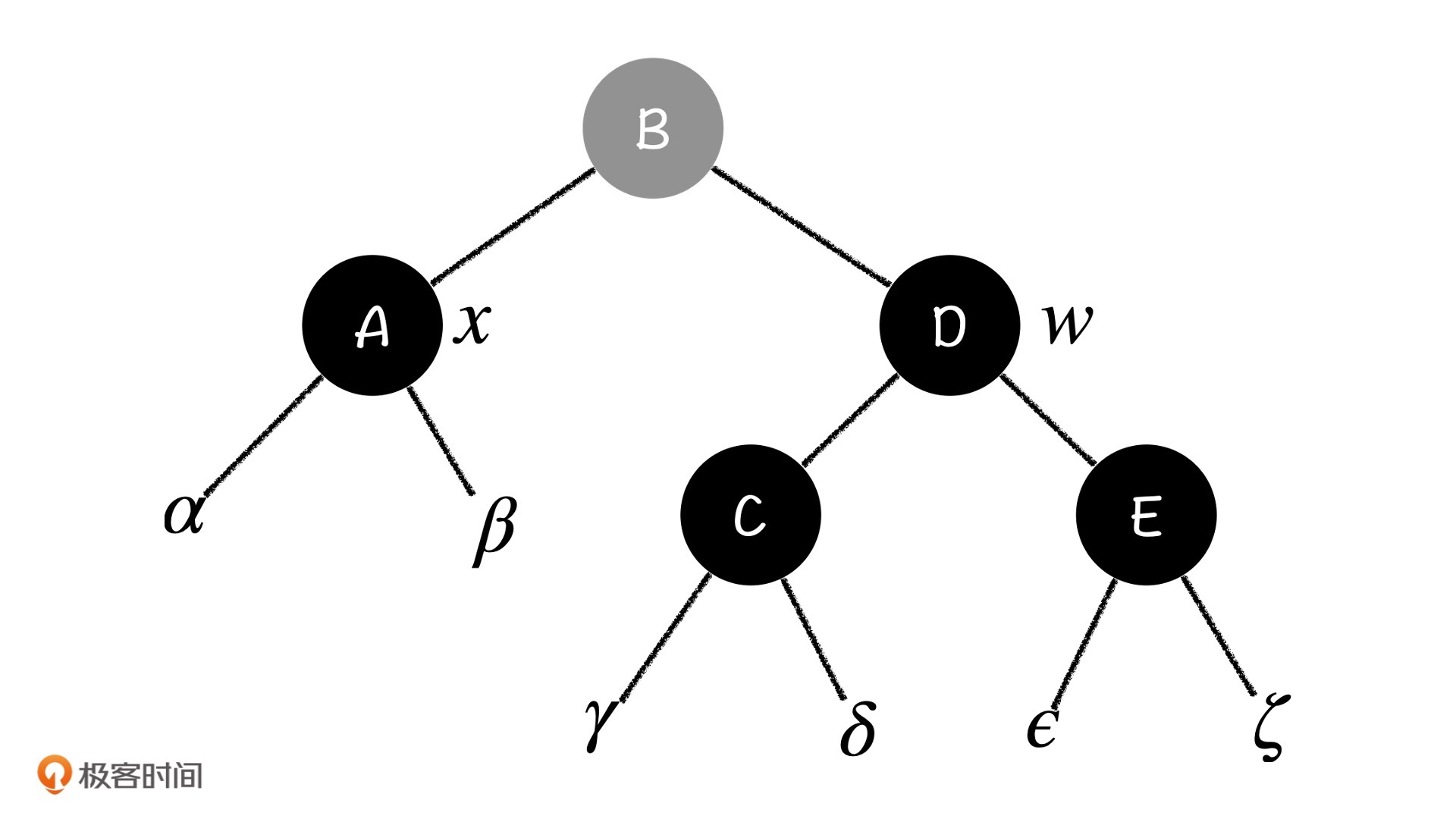
这种情况是最简单的。就像我们前面所说，x节点是个双黑节点，我们想要把它消解掉，则一定要从w中消解。而w的两个儿子都是黑的，所以我们把w节点变成红色之后，子树w的平衡就不会受到影响，又同时消解掉x的一个黑色，双黑节点的问题也就解决掉了。

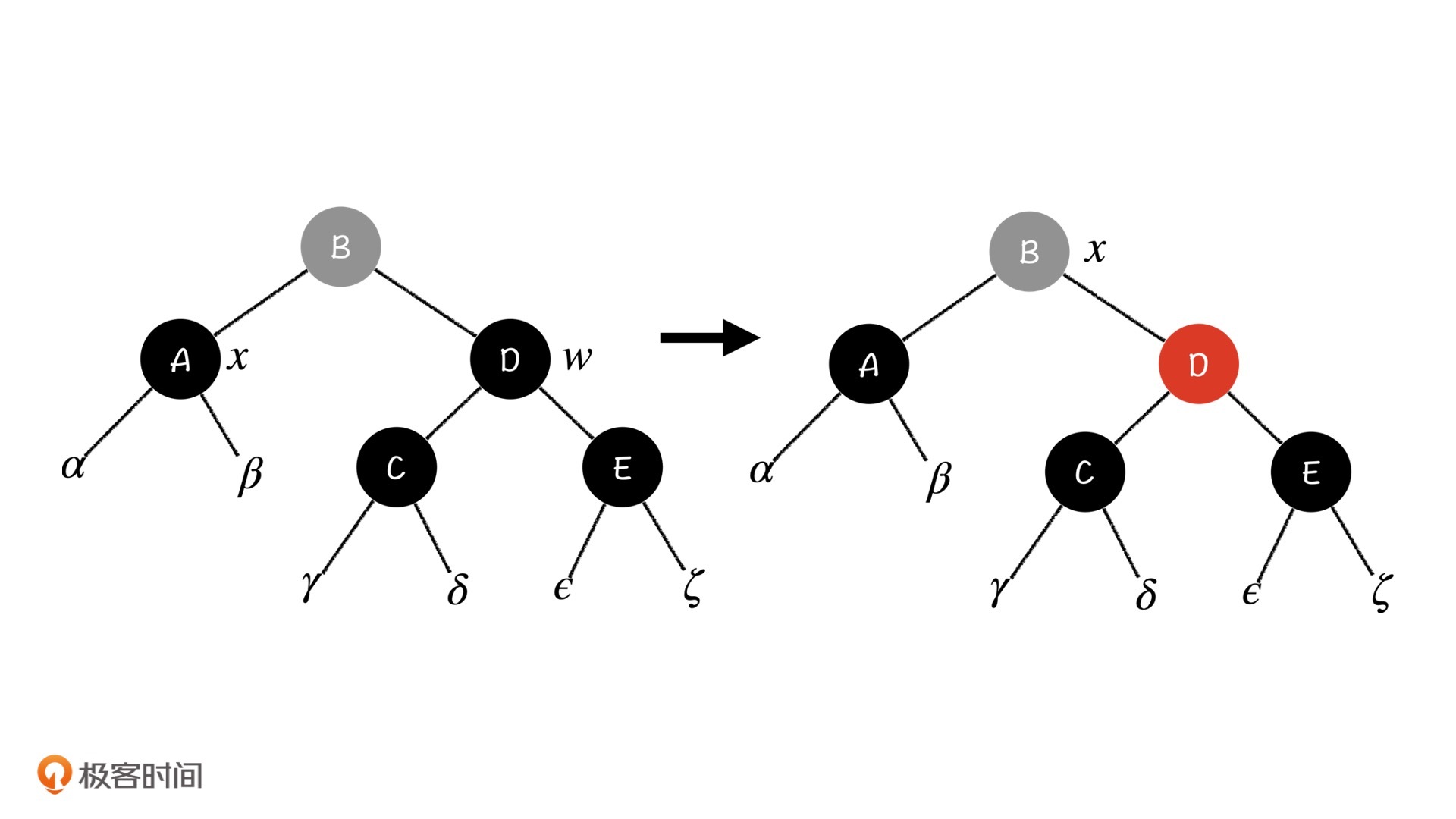
当然，与红黑树的插入操作一样，如果我们更改了D节点的颜色，就很有可能破坏它和B的性质，所以我们还要去检查它和B的关系。这个问题我们之前讨论过了，你可以自己思考一下。

Case 2：x节点的兄弟节点w是黑色节点，w的右孩子是红色节点

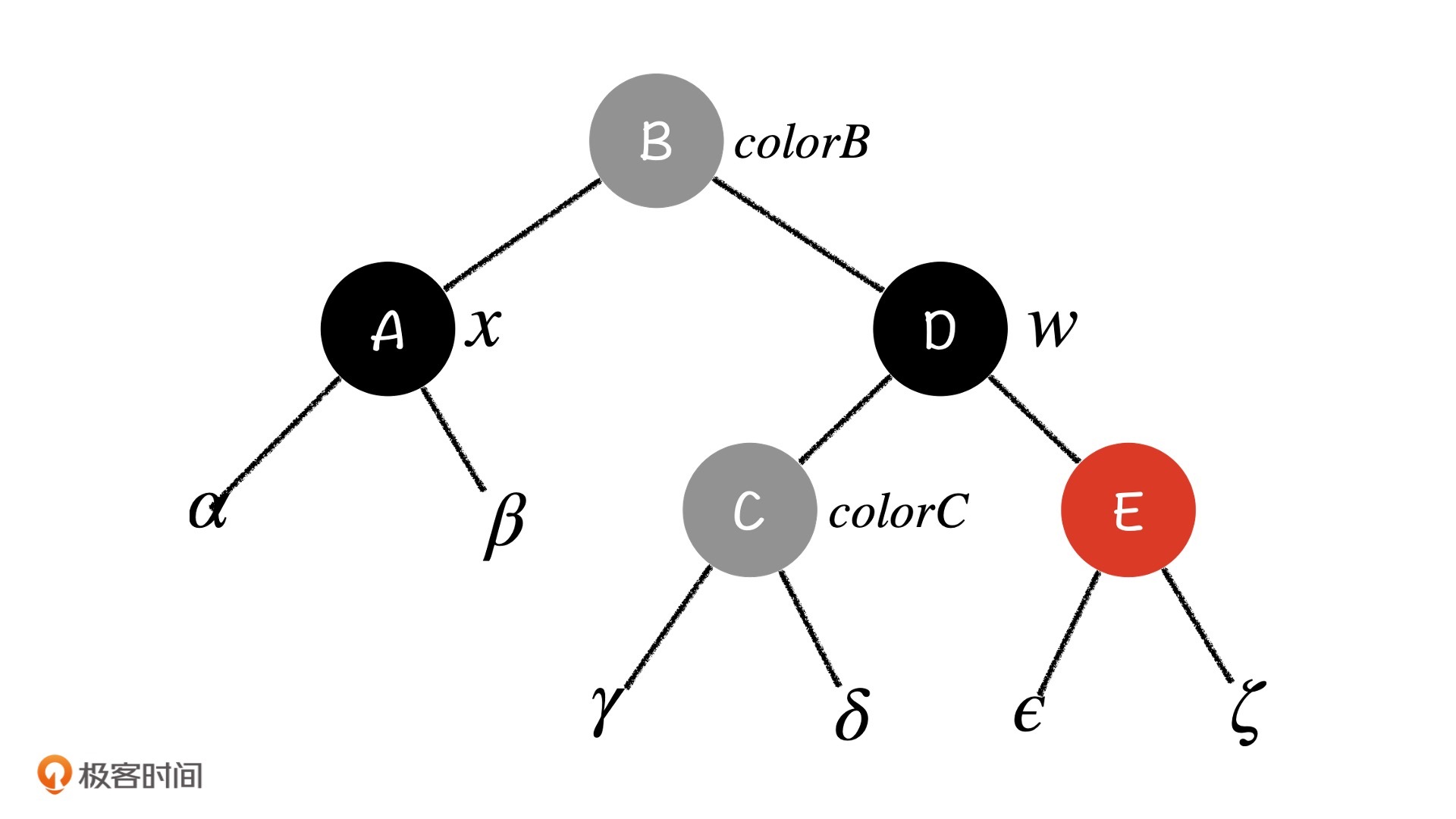
在这种情况中，我们还是想要利用红色节点分担掉x节点上多出来的那一重黑色。但是我们发现，红色节点E所处的位置很深，它是A节点兄弟节点的孩子节点，我们如果直接用E来分担，就必然会破坏掉整棵子树的性质。那怎么才能让E去分担这个黑色呢？

实际上，我们要先弄明白，E节点改变颜色是参照哪棵子树进行的。没错，就是它的兄弟，也就是以C为根的那棵子树。这个时候，我们发现可以通过旋转操作，让E节点的参照子树中有A节点。

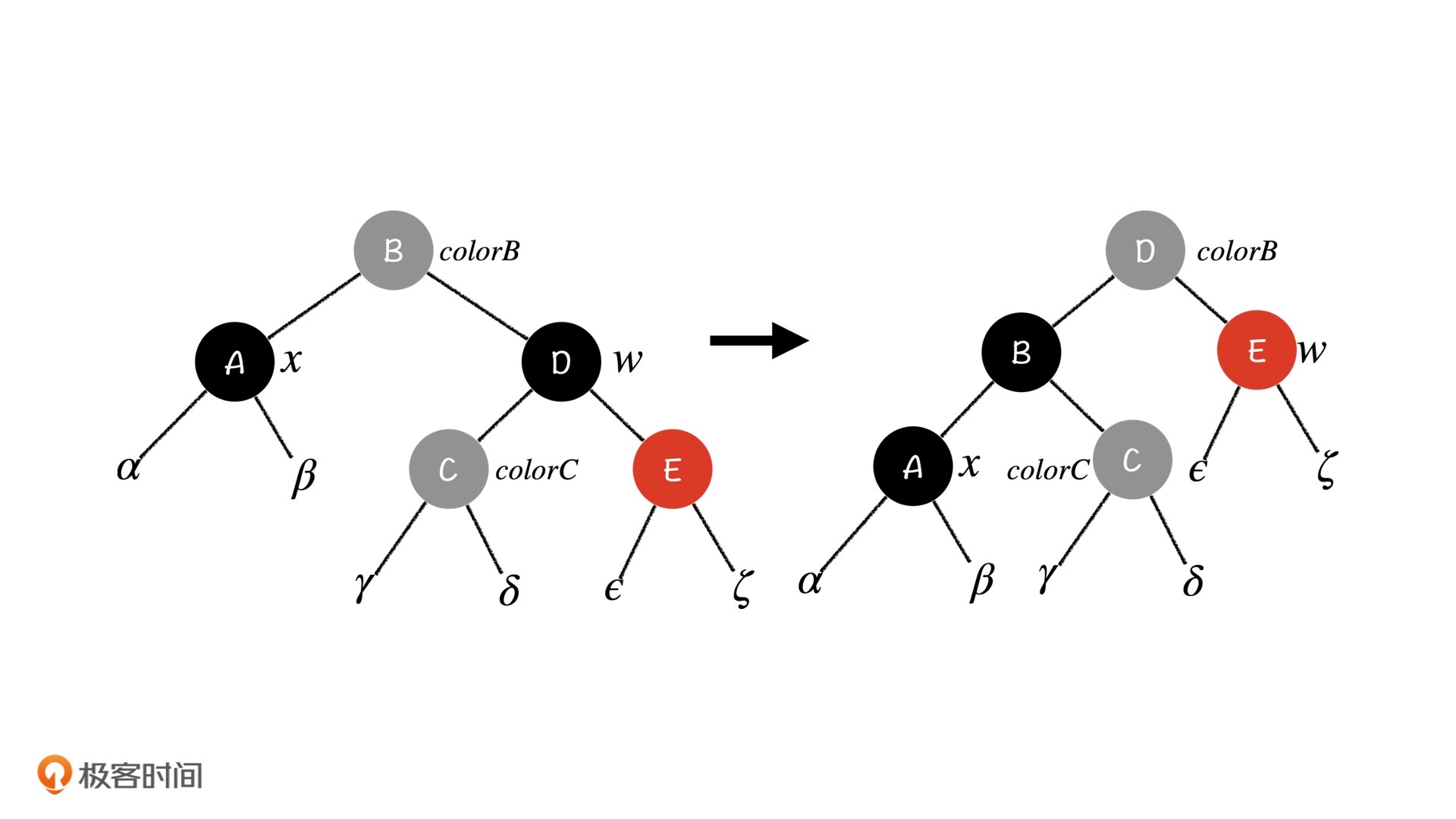
如上图，我们先进行了一次左旋操作，左旋之后又将D、B颜色互换，保持了C节点所在子树不受影响。这个时候，相比于初始情况，$\alpha$子树、$\beta$子树的阶（black height）多了一个，同时$\epsilon$子树、$\zeta$子树的阶又分别少了一个，所以E就可以直接分担A多出来的黑色了：我们将E染成黑色，再把A从特别黑变成黑色。最终子树的性质没有被破坏。

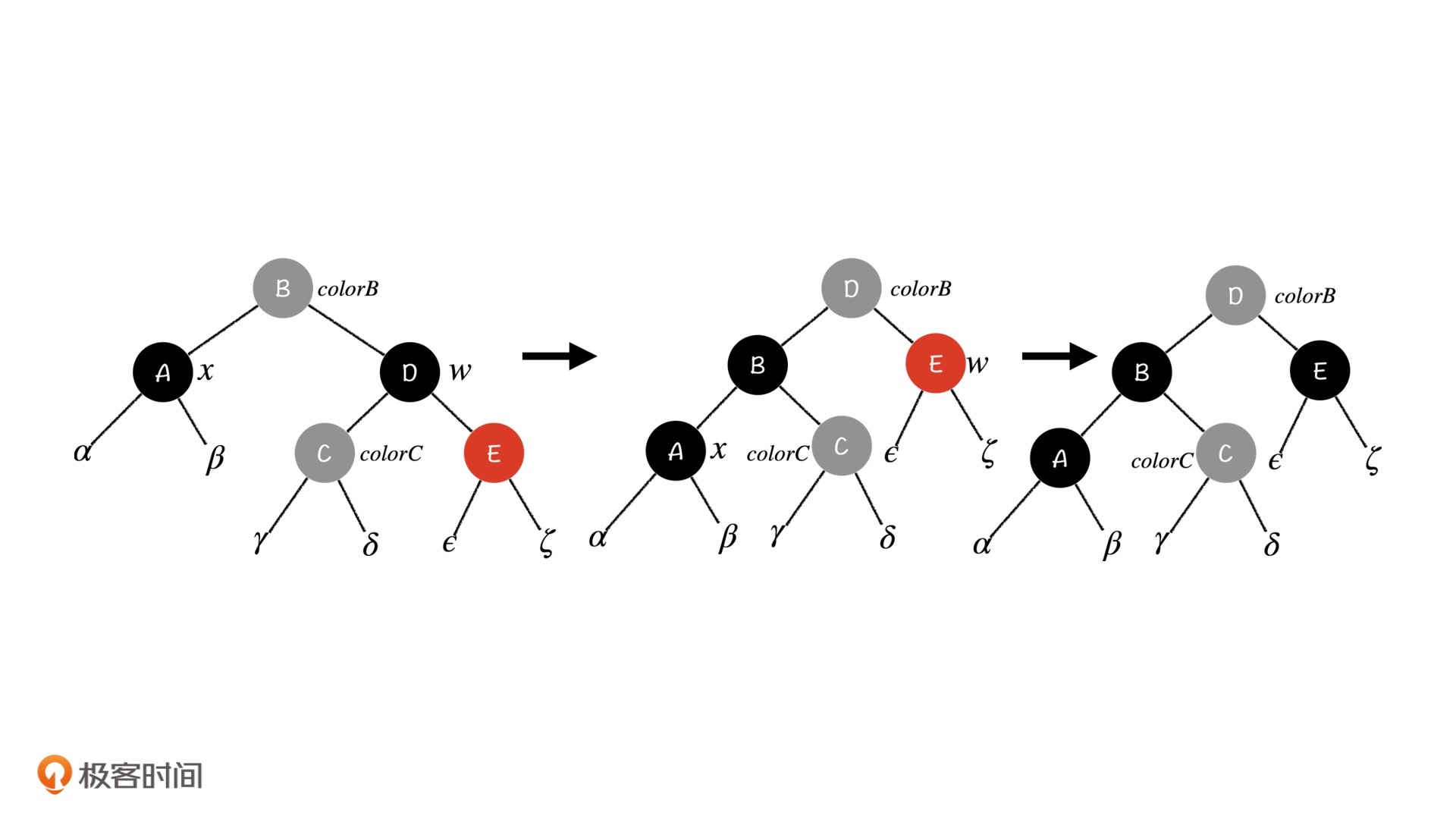
Case 3：x的兄弟节点w是黑色节点，w的左孩子是红色节点，右孩子是黑色节点

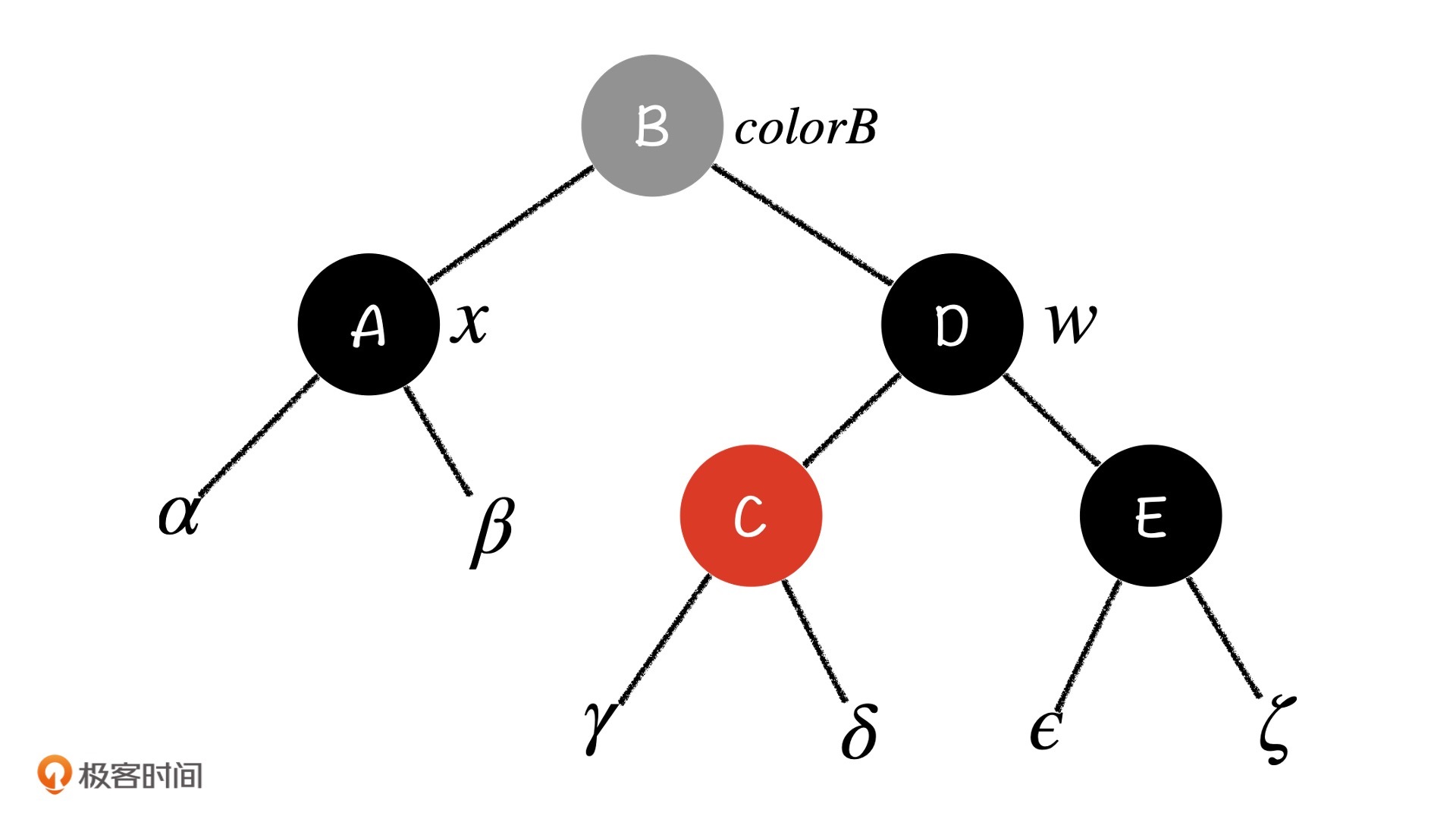
这次和第二种情况不同了，如果我们直接进行左旋操作，那么右子树中将没有任何可以找补的黑色节点，整棵树的平衡一定会被破坏掉。不过，在AVL树和红黑树的插入操作中，我们每次遇到这种情况，都可以先尝试把它归到我们熟悉的情况中，这样再去解决它就会容易很多。这次也一样，我们利用双旋操作来试着调整一下。

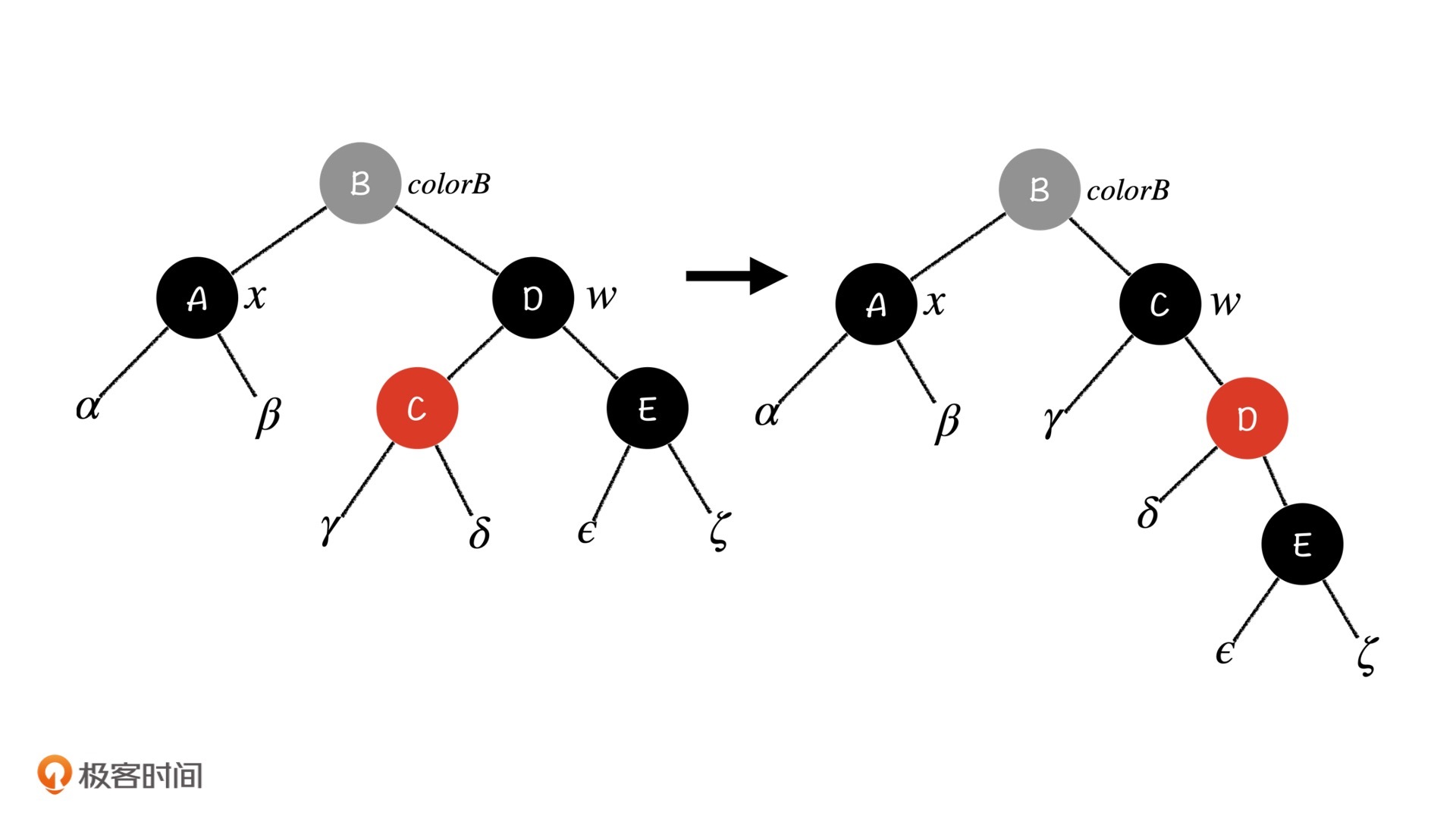
结合上面这张图，我们可以先通过右旋将红色节点变成w的右子节点，把它归化到第二种情况中。然后，我们再对D节点进行一次右旋。同时，为了保证$\gamma$子树和$\delta$子树的性质，我们将C节点和D节点的颜色交换一下。这样一来，这种情况就成功归化到了第二种情况中，我们用第二种情况的方法去解决它就好了。

现在，我们已经解决双黑节点x的兄弟节点是黑色节点的所有情况了，下面，我们再来看最后一种情况。

Case 4：x的兄弟节点w是红色节点

如果x的兄弟节点w是红色节点，那么根据性质4，它们的父亲节点就一定是黑色节点，且w的孩子节点一定也是黑色节点。

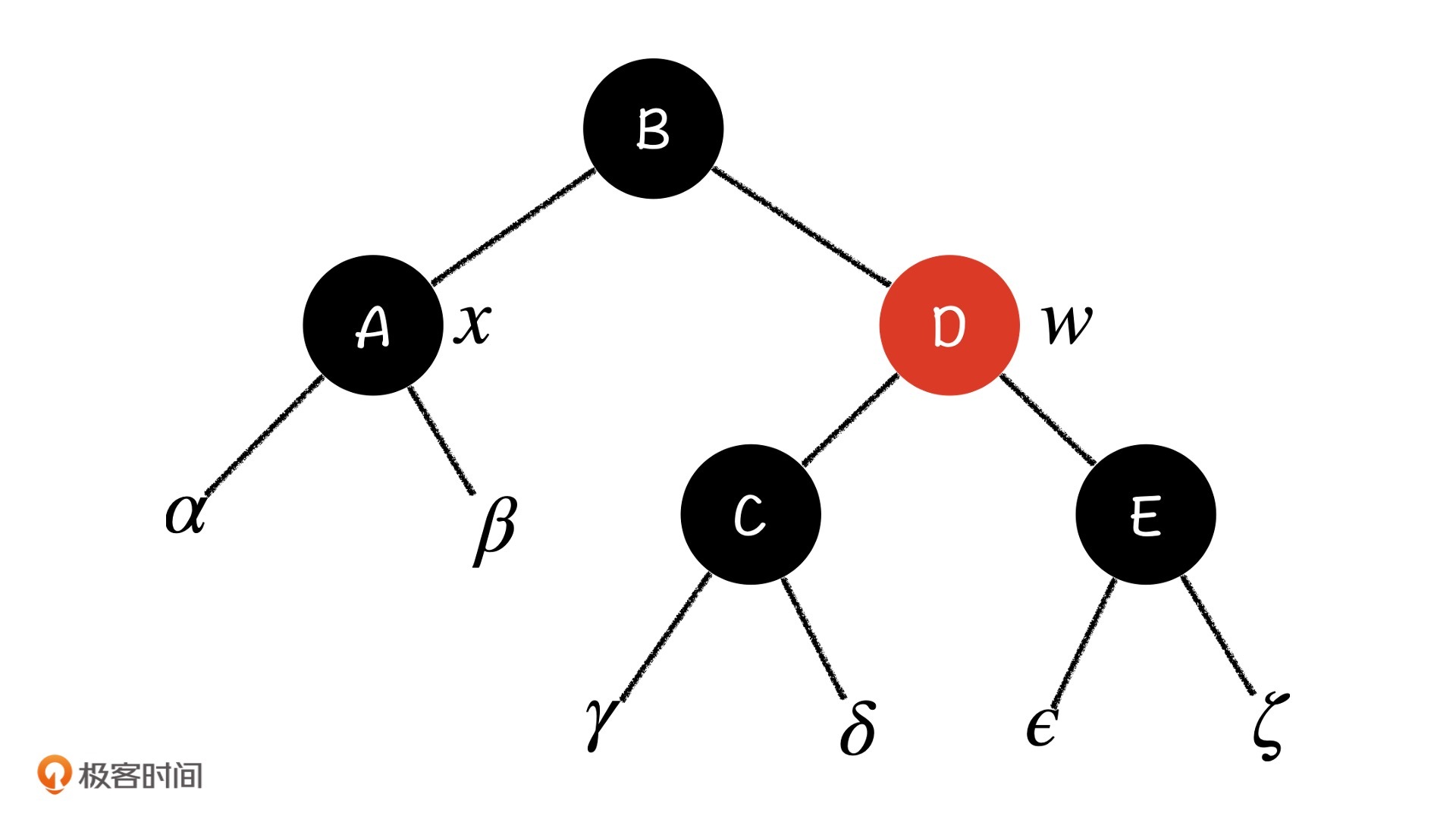
这种情况下，如果我们直接拿兄弟节点w去分担x节点的黑色，w的节点D和E的平衡会受到影响，整棵子树的性质5会被打破，所以我们就要继续考虑能否通过旋转操作，让这个问题得以解决。而我们看到上图的结构，如果直接进行右旋，A节点成为根节点，则所有子树的性质5都会被打破，这种情况调整起来就更加复杂了，所以我们只能对B进行右旋，尝试后的结果如下：

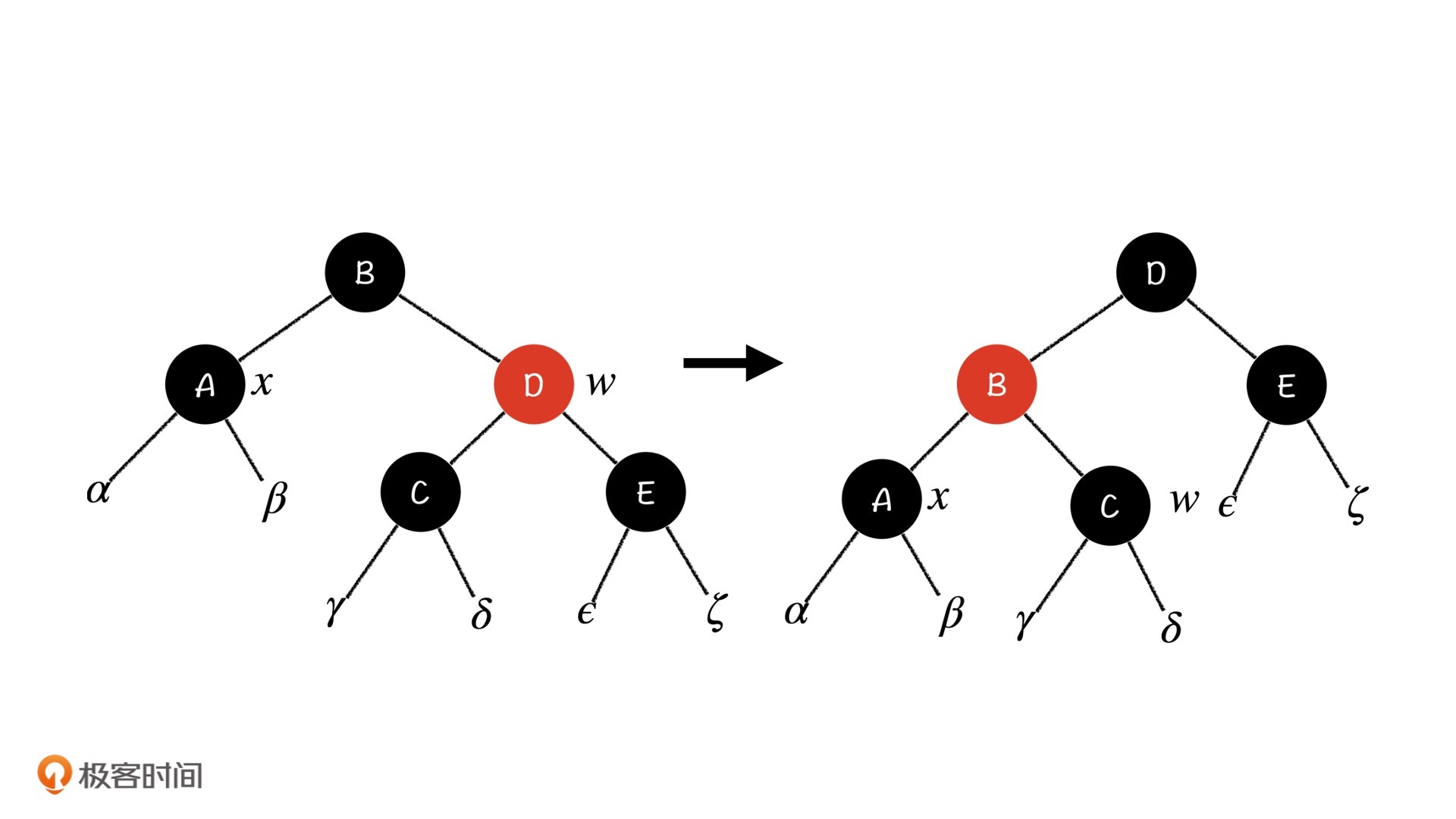
右旋之后，同样是为了保持平衡，我们将D节点染成黑色，将B节点染成红色。

发现了吗？双黑节点的兄弟节点变成了一个黑色节点，所以这种情况被归化到前三种情况的任意一种了。我们直接利用之前的方法，按图索骥就可以解决这种情况。

课程小结

到这里，红黑树相关的内容我们就彻底讲完了。这节课，我们一起学习了红黑树的删除操作。

在删除操作的整个过程中，我们都是在围绕着如何解决双黑节点进行的。双黑节点的产生情况，其实就是被删除的节点z只有一个孩子x，并且x是黑色。

想要完全消解掉双黑节点，我们要分4种情况讨论：

• x的兄弟节点以及它的两个儿子都是黑色节点；
• x的兄弟节点是黑色节点，而它的右孩子是红色节点；
• x的兄弟节点w是黑色节点，w的左孩子是红色节点，右孩子是黑色节点；
• x的兄弟节点w是红色节点。

总的来说，调整的原则其实就两个，一个是改变节点的颜色，另一个是进行旋转操作。如果遇到了不熟悉的情况，我们可以先尝试把它归到我们熟悉的情况中，这样再去解决它就会容易很多了。比如，我们会常用到双旋操作。

不得不说，红黑树的操作相对来讲，不仅情况繁多，而且操作也比较复杂。但我们实际上只需要在局部进行调整操作，很少涉及大规模的调整，所以红黑树依然可以保持着较低的更新成本。

同时，你可能也发现了，在删除操作中，我们不断用红色节点补充缺失的黑色节点，所以在删除操作中，红色节点会变得越来越少，红黑树也就越来越向AVL树发展。这也是我们在红黑树插入的时候默认被插入节点是红色节点的原因之一。

实际上，红黑树虽然经常出现在计算机应用的各个角落，看上去我们只需要调包就可以使用它，但由于它较为复杂的情况，我们理解它的同时也在一定程度上锻炼了我们的算法思维，所以红黑树的原理以及相关操作，也是各大公司在面试的时候的热门问题。因此，我们用了2节课去推导红黑树的各项性质，以及各种操作，就是希望你能去理解它，而不是仅仅去记忆它。

课后练习

1. 如果某一个节点被插入到红黑树之后，立刻被删除了，那么红黑树的形态和插入节点之前一样吗？
2. 红黑树是存在哪些高效的级联算法吗？如果有，可以在留言区分享出来。

好啦，关于红黑树的插入和删除操作，你都理解了吗？可以在留言区写下你的疑惑，也希望你能把这节课的内容转发出去。那今天就到这里了，我是胡光，我们下节课见！