04 | 堆排序:体会线性建堆法的威力
你好,我是胡光,欢迎回来。
上节课,我们讲了堆这种维护集合中最值的高效数据结构,也留下了一道经典的算法题,蚂蚁问题。这节课,我们一起来看看怎么利用堆来解决它。
我们先回顾一下上节课的问题。
假设现在有一个水平面,上面有8只蚂蚁排成一排,我把这张示意图放在了文稿中。方便起见,我们给所有的蚂蚁从左到右依次编号,编号为 1 到 8。从0秒开始,红色蚂蚁向左爬,蓝色蚂蚁向右爬,爬行的速度都是1m/s。如果有 2 只蚂蚁迎面碰到以后,这 2 只蚂蚁不会做任何的感情交流,而是会立刻掉头向相反方向继续爬行。而爬行到桌子边沿的蚂蚁,会从桌子上掉下去。问:有哪些蚂蚁会从左边掉下去,又有哪些蚂蚁会从右边掉下去?
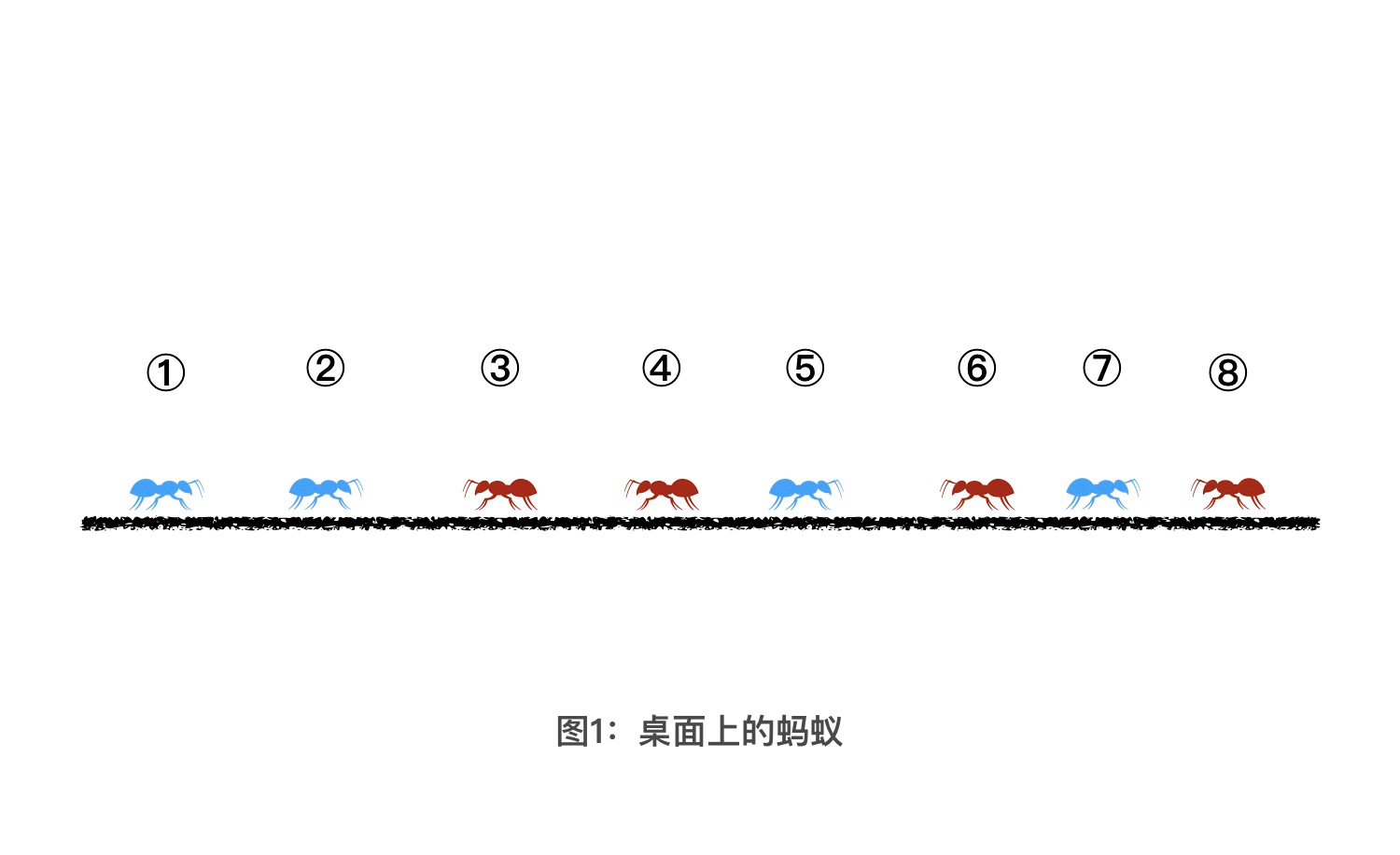
怎么解决蚂蚁问题?
要搞定蚂蚁问题,首先你需要把自己带入到问题场景中,只有充分理解了问题场景,才能更好地解决这个问题。下图是一个蚂蚁问题的具体场景:

从图中我们可以看出,2、3 号蚂蚁会相撞,5、6 号蚂蚁会相撞,7、8号蚂蚁也会相撞。因为相撞以后的两只蚂蚁的方向会改变,所以 2、3 号蚂蚁相撞以后,2 号蚂蚁会向着 1 号蚂蚁所在的方向行进,3号蚂蚁会向着4号蚂蚁所在的方向行进。这样,在之后的某个时刻,1、2 号蚂蚁,3、4 号蚂蚁就会相撞。
那要想知道最终有哪些蚂蚁会分别从左、右两边掉下去,一种最基本的解法,就是根据时间顺序来模拟蚂蚁们的相撞过程。具体怎么做呢?下面,我们先模拟分析一下这4只蚂蚁的相撞过程。
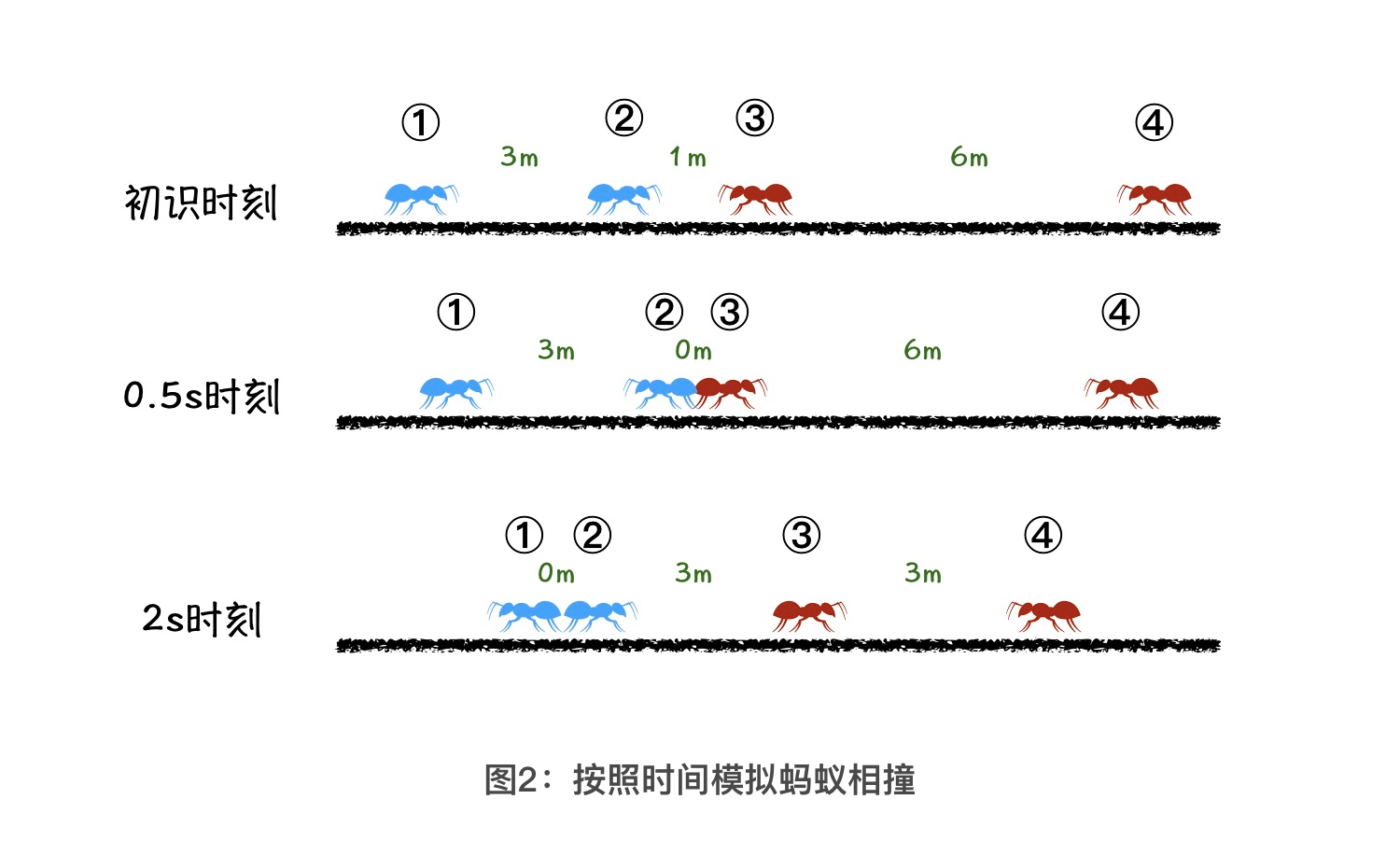
如图所示,一共有4只蚂蚁,我们从1到4给它们编号。最开始,它们之间的距离分别是3米、1米 和 6米。其中,2号和3号离得最近,并且方向相对。因为蚂蚁的移动速度是1m/s,所以2号和3号会在 0.5s 的时刻相撞,然后它们会向相反方向爬去。
这个时候,1号和2号方向相对、3号和4号方向相对,并且1号和2号距离最近。所以下一次最先相撞的,应该是在1、2号蚂蚁.通过计算我们能知道,它们会在 2s 的时刻相撞。相撞之后,2、3号蚂蚁同向而行,3、4号蚂蚁相向而行。
由此我们能得出一个结论,想要模拟蚂蚁相撞的过程,我们就要找到当前时刻距离最近的两只相向而行的蚂蚁。请你注意这句话:我们要找到当前时刻距离最近的两只相向而行的蚂蚁。那在一堆距离数据中,每次找到一个最小的距离,这不就是小顶堆的经典应用场景吗?因此,解决这个问题的关键,就是使用小顶堆来存储当前桌面上所有相向而行的蚂蚁之间的距离。
1. 用小顶堆解决蚂蚁问题
确定了使用小顶堆以后,我们又要面临一个新问题,那就是相向而行的蚂蚁之间的距离会随着时间而变化。就像两只蚂蚁一开始的相对距离是6米,下一秒就可能会变成5米。而我们现阶段所掌握的堆结构,并不支持存储动态更新的数据。这该怎么办呢?
其实解决起来也很简单,只要我们存储在堆中的是两只蚂蚁在固定时刻的相对距离,比如 0 时刻,我们就可以不用更新堆中的数据。
需要注意的是,两只蚂蚁在时刻 0 时的相对距离,不是指时刻 0 时这两只蚂蚁的真实距离,而是逻辑距离。这两个距离有什么不同呢?我们还是通过一个具体的例子来理解。
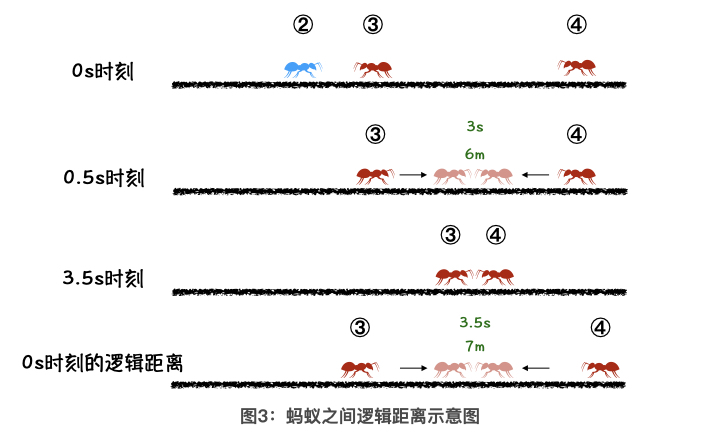
如上图所示,在 0s 的时候,3、4号蚂蚁是同向而行的,距离是6米。在 0.5s 的时候3号蚂蚁发生了转向,这个时候3、4号蚂蚁开始了相向而行。此时,3、4号蚂蚁之间的实际距离是6米,也就意味着,它俩会在 3.5s 的时候相遇。
这个时候,我们从逻辑上面让两只蚂蚁退回去,它们会以每秒钟 2 米的速度远离对方。也就是说,在 0s 的时候,逻辑上这两只蚂蚁的距离应该是 7m,所以我们存储到堆中的数据应该是逻辑上的 7m,而不是 3、4 号蚂蚁在 0s 时候的实际距离 6 米。
理解这一步的重点,在于理解堆中的数据是不可以动态更新的,所以我们要将两只蚂蚁在0时刻的逻辑距离存储到堆中。当然你也可以直接将两只蚂蚁相遇的绝对时间存储在堆中,作为堆中元素排序的依据,然后按照蚂蚁相遇的绝对时间,来模拟蚂蚁们的相撞顺序。这样,我们就能得到蚂蚁们全部相撞后的爬行顺序了。
到这里,我们就讲完了如何用模拟的方法来解决蚂蚁问题。其实解决的核心就在于用堆来维护蚂蚁之间相撞的顺序。
2. 蚂蚁问题最快的解法
实际上,除了使用小顶堆,蚂蚁问题还有一种更简单的解决方式,那思路是什么呢?其实一句话就能说明白:一只向右走的蚂蚁和一只向左走的蚂蚁碰撞之后,会变成一只向左走、一只向右走。也就是说,碰撞并不会改变桌面上向左和向右的蚂蚁总数。
而且通过前面的分析,你也会发现,无论怎么碰撞,蚂蚁之间的相对顺序是不会改变的(不管怎么碰撞,蚂蚁的顺序不会改变)。最后,只有向左走的蚂蚁,才有可能从左边的桌子边掉下去,向右走的蚂蚁会从右边的桌子边掉下去。所以在图1中,一开始有4只蚂蚁是向左走的,也就意味着,最后1、2、3、4这四只蚂蚁会从左侧桌子掉下去,剩余的蚂蚁会从右侧桌子掉下去。
怎么样,上面这种方法,是不是比用小顶堆模拟的方式更容易理解和实现呢?你可能要问了,那我们为什么还要学习小顶堆这种更麻烦的解决方案呢?这就好比,你现在的目标是要画一个圆,我可以选择给你一个印章,你只需要用印章往纸上盖一下,就会得到一个圆。可如果将来,你面对的任务是画一个正方形,又该怎么办呢?因此,你真正需要的是一支笔,而不是一个固定形状的印章,而小顶堆就是这支笔。今天呢,我们就是在锻炼这支笔的使用方式。我也希望,今后如果碰到画正方形或者三角形之类的问题,你能想起来使用这支笔。
堆排序
搞定了蚂蚁问题以后,我想再和你说说,由堆衍生出来的一种排序算法,堆排序。
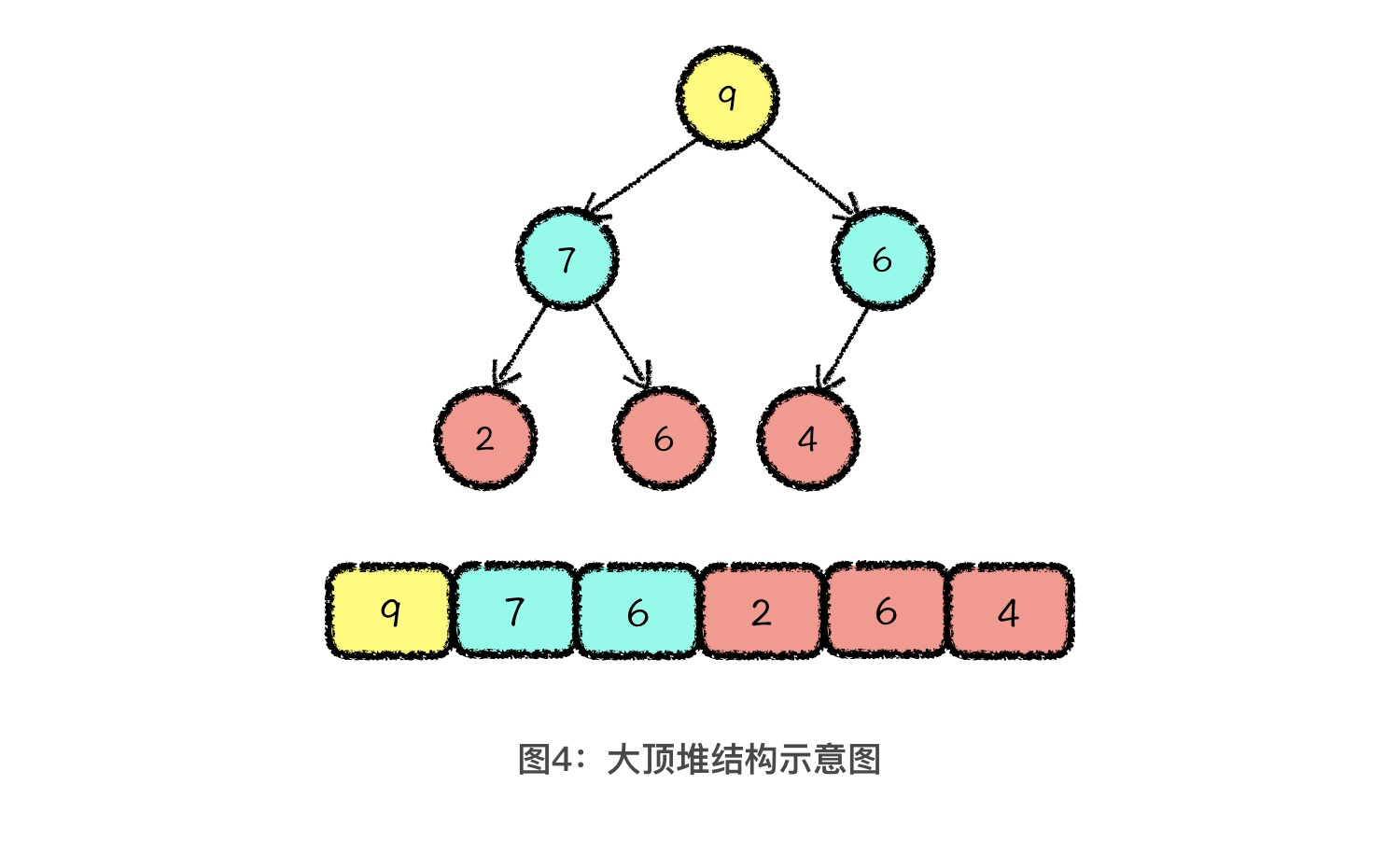
那堆排序怎么理解呢?我们还是先看一个例子。假设我们要对一个数组从小到大进行排序,首先我们可以将原数组中的数据建立成一个大顶堆。这样,最大的元素就会在数组的首位,大顶堆的存储结构如上图。正常情况下,从堆中删除一个元素,是直接将堆顶元素弹出,然后将堆中最后一位的元素放到堆顶,再做向下调整的。这样的话,原来堆中的末尾元素位置就空了出来。
现在,由于要对原数组进行排序,因此我们可以把弹出的堆顶元素与堆中的末尾元素进行位置交换,再向下做调整。也就是将图中的元素9和4做调换,再对4做向下调整。经过一轮这样的操作,我们就可以将一个堆顶的最大值放到正确的排序位置上。我在下图中给出了三轮操作以后,数组中元素的排序情况:
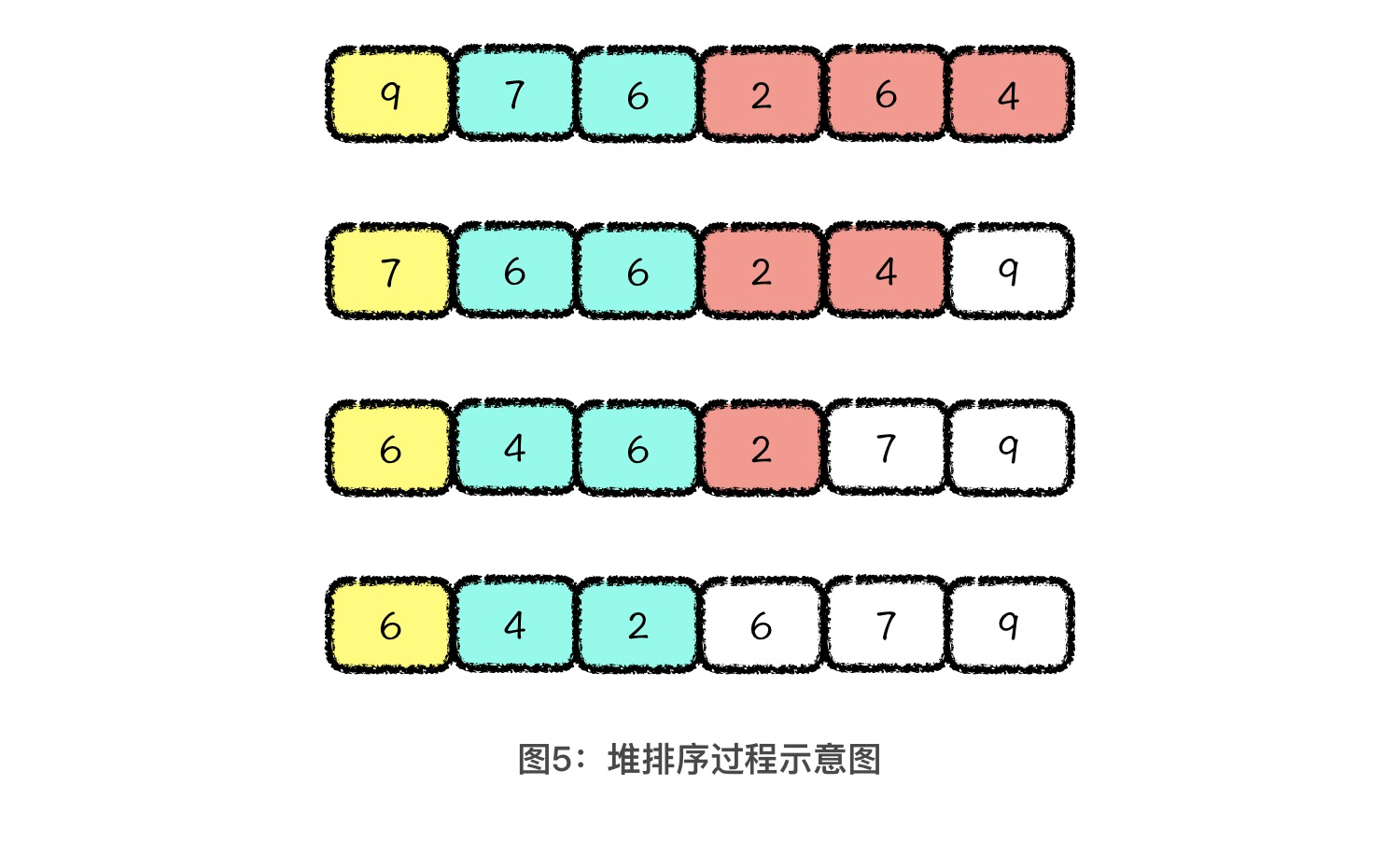
如图所示,经过三轮弹出大顶堆顶元素的操作以后,原数组中最大的三个值就被放置到了最后三位。当大顶堆中元素弹空时,也就完成了对原数组排序的过程。
好了,那我们来总结一下堆排序的流程:
- 在原数组上建立堆结构
- 将堆顶元素与堆末元素进行调换,再对堆顶元素进行向下调整
- 经过 n 轮操作以后,数组中的元素就有序了
通过我前面的解释,相信你应该已经理解第2、3步了,它们操作起来非常简单,我就不再细说了。而对于第 1 步,如果想在一个数组上建立一个堆结构,我们要怎么做呢?
一种最直接的方式,就是我们先将原数组分成两部分,前半部分是堆,后半部分是数组中的元素。然后通过堆的向上调整策略,我们依次将后面的元素插入到前面的堆结构中。下图展示的就是用这种尾插法建堆的前三轮数组中的元素情况:
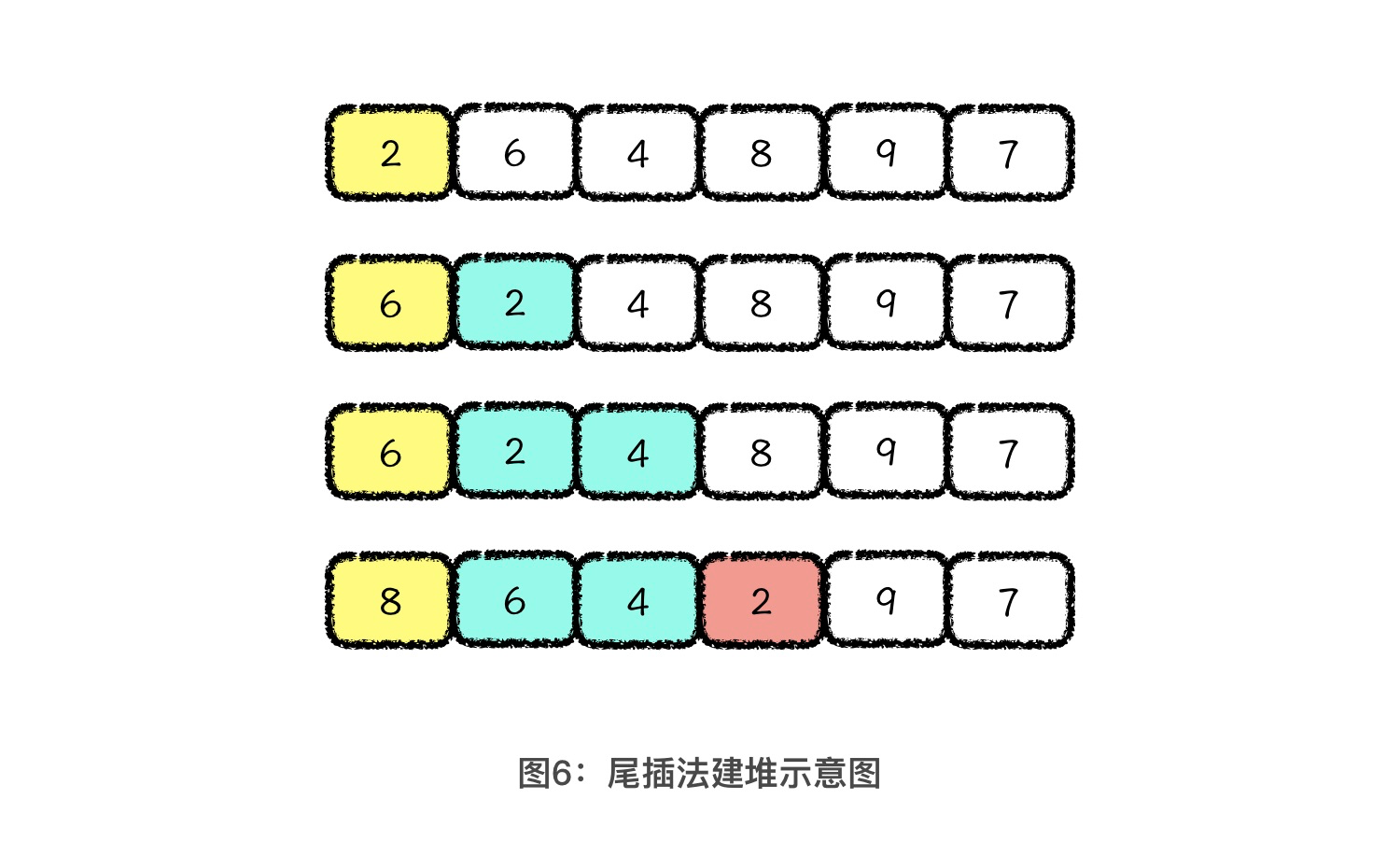
这种建堆的方法比较直观,所以建堆的时间复杂度我们很容易就可以计算出来,就是 O(nlogn)。到这里,我们就算是掌握堆排序的整个流程了。
堆排序优化:线性建堆法
其实,对于堆排序中建堆的这个流程,我们还可以再优化,优化的方法叫做线性建堆法。线性建堆法就是将原数组分成两半部分,前半部分是数组部分,后半部分是已经建好的堆,然后采用向下调整的方式,从后向前依次将数组中的元素调整到堆中。如下图所示:
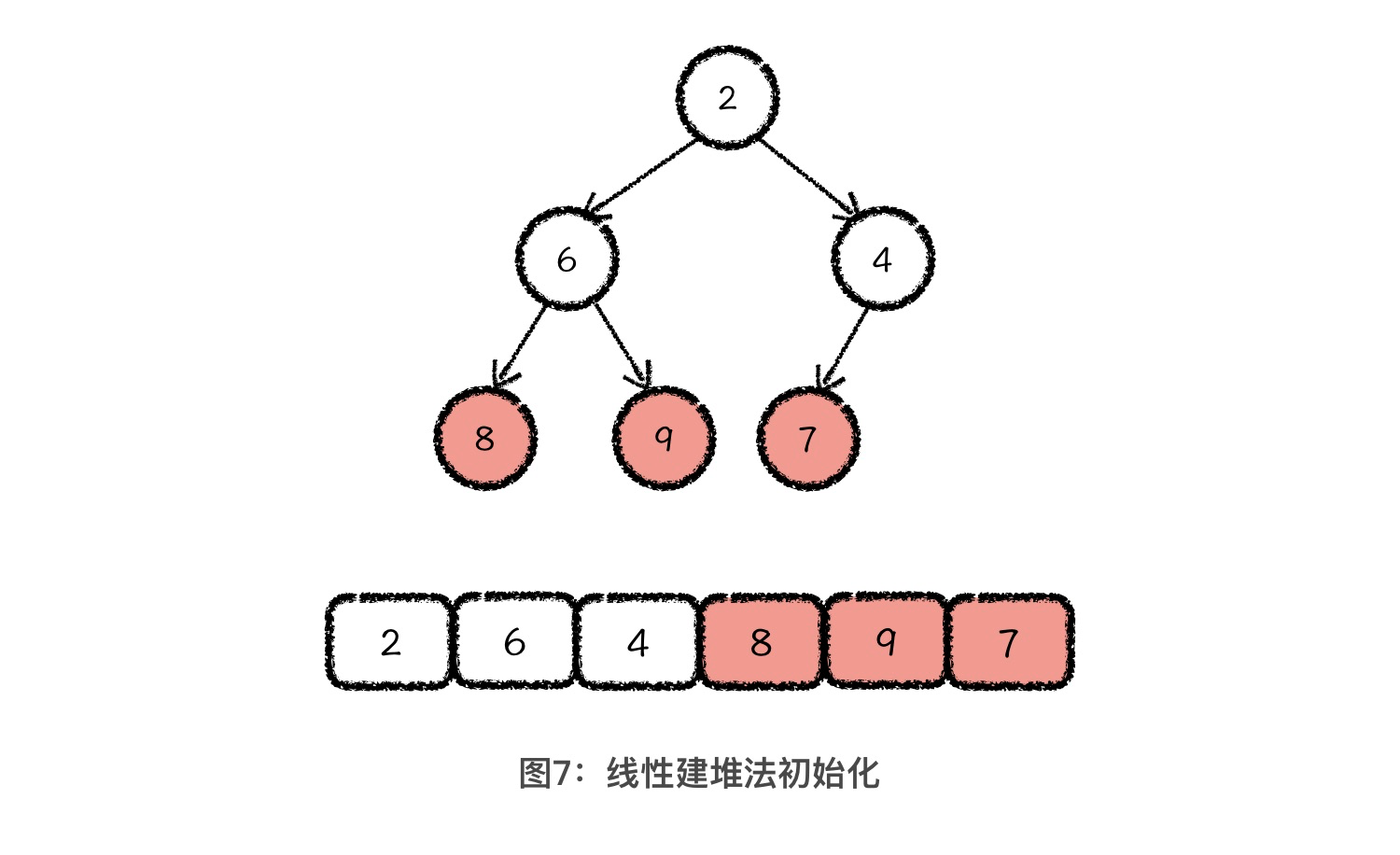
因为在上图这个数组中,处在堆中最下一层的 8、9、7这 三个节点,已经无法向下调整了,所以我们在初始化的时候,就直接把它们三个当成是已经调整好的堆结构就好了。之后,我们从元素4开始,向前依次将4、6、2三个元素进行向下调整,插入到他们下面的堆结构中。具体的过程,你直接参考正常的堆结构向下调整过程就可以理解了,我就不细说了。
事实上,这种所谓的线性建堆法,用的就是向下调整策略。而之前我们学习的尾插法,用的是向上调整。两者好像没有太大的区别。那怎么能说线性建堆法比尾插法要优化呢?下面,我们来简单分析一下它们的时间复杂度,你就能明白了。
首先,假设堆中的节点数量是 n,那么树高就是 $log_{2}{n}$。其中,根节点可能需要向下调整 $log_{2}{n}$次。根节点下面的2个子节点,可能需要向下调整 $log_{2}{n} - 1 $次,第三层的4 个子节点,可能需要调整$ log_{2}{n} - 2 $次。也就是说,有 $2^i $个节点,可能需要向下调整 $log_{2}{n} - i $次。最后,我们算出所有节点需要调整的总次数,就能得到如下式子:
$$
\begin{array}{c}
\operatorname{sum}=1 \times \log _{2} n+2 \times\left(\log _{2} n-1\right)+4 \times\left(\log _{2} n-2\right) \ldots \\\
2 \operatorname{sum}=2 \times \log _{2} n+4 \times\left(\log _{2} n-1\right)+8 \times\left(\log _{2} n-2\right) \ldots \\\
2 \operatorname{sum}-\text {sum}=2+4+8+\ldots+\left(2^{\log _{2} n}=n\right)-\log _{2} n \\\
\approx 2 n
\end{array}
$$
因此,线性建堆法之所以称为线性,是因为时间复杂度真的为 O(n)。总之,线性建堆法的思想很好理解,因为在二叉树中,每向下一层节点数量就会翻一倍。所以在线性建堆法中,如果某一层包含的节点数量越多,那这一层中每个节点的调整次数就越少。这样,我们就能尽可能保证整体效率的最优。用一句话总结就是“让少数人多动,多数人少动”。
课程小结
今天,我们用两种方法解决了蚂蚁问题。
第一种是利用小顶堆结构,来维护最近相撞的两只蚂蚁的距离,模拟出蚂蚁的相撞过程,确定最终的蚂蚁排序。第二种方法类似脑筋急转弯比较取巧,你只需了解就可以了。
除此以外,我们还学习了堆排序算法以及一种更高效的建堆方式线性建堆法。线性建堆法思想简单来说,就是利用向下调整策略,当节点越多的时候,我们的调整次数就越少。因此,它的时间复杂度是 O(n)。
最后,我希望你通过今天的学习,能够记住用堆解决蚂蚁问题的过程,以及推导线性建堆法的时间复杂度的过程。这会对你之后的学习和工作,非常有帮助。
课后练习
因为蚂蚁问题是一个锻炼思维方式的好题目。所以,我希望你能深入去想一想,如果蚂蚁问题不是发生在桌面上,而是在一个圆环上的话。那经过 n 秒以后,你能输出每个蚂蚁的位置吗?欢迎在留言区把你的思考和具体做法写下来,我们一起讨论。
如果你身边的朋友也被类似的问题“难住”过,那就快把这节课分享给他吧!今天就到这里,我是胡光,我们下节课见!