19 | 如何用着色器实现像素动画？

你好，我是月影。

上节课，我们以HTML/CSS为例，讲了三种动画的实现方法，以及标准的动画模型。我们先来回顾一下：

固定帧动画：为每一帧准备一张图片，然后把CSS关键帧动画的easing-function设为step-end进行循环播放。
增加增量动画：在每帧给元素的相关属性增加一定的量，比如增加一个rotate角度。
时序动画：通过控制时间和动画函数来描述动画，首先定义初始时间和周期，然后在update中计算当前经过时间和进度p，最后通过p来更新动画元素的属性。
标准动画模型：先定义Animator类，然后使用线性插值实现匀速运动的动画，以及通过缓动函数实现变速运动的动画。

而WebGL实现动画的方式和以上这些方式都有差别。所以这节课，我们就接着来讲怎么用着色器来实现动画。

因为实现固定帧动画最简单，所以我们还是先来说它。

如何用着色器实现固定帧动画

我们完全可以使用在片元着色器中替换纹理坐标的方式，来非常简单地实现固定帧动画。为了方便对比，我还是用上一节课实现会飞的小鸟的例子来讲，那片元着色器中的代码和最终要实现的效果如下所示。

#ifdef GL_ES
    precision highp float;
    #endif
    
    varying vec2 vUv;
    uniform sampler2D tMap;
    uniform float fWidth;
    uniform vec2 vFrames[3];
    uniform int frameIndex;
    
    void main() {
      vec2 uv = vUv;
      for (int i = 0; i < 3; i++) {
        uv.x = mix(vFrames[i].x, vFrames[i].y, vUv.x) / fWidth;
        if(float(i) == mod(float(frameIndex), 3.0)) break;
      }
      vec4 color = texture2D(tMap, uv);
      gl_FragColor = color;
    }

利用片元着色器实现固定帧动画的关键部分，是main函数中的for循环。因为我们的动画只有3帧，所以最多只需要循环3次。

我们还需要一个重要的参数，vFrames。它是每一帧动画的图片起始x和结束x坐标，我们用这两个坐标和vUv.x计算插值，最后除以图片的总宽度fWidth，就能得到对应的纹理x坐标。替换纹理坐标之后，我们就能实现一个会飞的小鸟了。

实现这个固定帧动画对应的JavaScript代码如下：

const canvas = document.querySelector('canvas');
    const renderer = new GlRenderer(canvas);
    const textureURL = 'https://p.ssl.qhimg.com/t01f265b6b6479fffc4.png';
    (async function () {
      const texture = await renderer.loadTexture(textureURL);
      const program = renderer.compileSync(fragment, vertex);
      renderer.useProgram(program);
      renderer.uniforms.tMap = texture;
      renderer.uniforms.fWidth = 272;
      renderer.uniforms.vFrames = [2, 88, 90, 176, 178, 264];
      renderer.uniforms.frameIndex = 0;
      setInterval(() => {
        renderer.uniforms.frameIndex++;
      }, 200);
      const x = 43 / canvas.width;
      const y = 30 / canvas.height;
      renderer.setMeshData([{
        positions: [
          [-x, -y],
          [-x, y],
          [x, y],
          [x, -y],
        ],
        attributes: {
          uv: [
            [0, 0],
            [0, 1],
            [1, 1],
            [1, 0],
          ],
        },
        cells: [[0, 1, 2], [2, 0, 3]],
      }]);
      renderer.render();
    }());

实际上WebGL实现固定帧动画的思路，和上一节课的思路是类似的。只不过，上一节课我们直接用CSS的background-image，来切换background-position就可以实现动画。而在这里，我们需要将图片纹理tMap传进去，然后根据不同的frameIndex来计算出对应的纹理坐标，并且这个计算是在片元着色器中进行的。

如何用着色器实现非固定帧动画

好了，知道了怎么实现固定帧动画。接着，我们再来说增量动画和时序动画的实现。由于这两种动画都要将与时间有关的参数传给着色器，处理过程非常相似，所以我们可以将它们统称为非固定帧动画，放在一起来说。

用Shader实现非固定帧动画，本质上和上一节课的实现方法没有太大区别。所以，我们仍然可以使用同样的方法，以及标准动画模型来实现它。只不过，用Shader来实现非固定帧动画更加灵活，我们可以操作更多的属性，实现更丰富的效果。下面，我们详细来说说。

1. 用顶点着色器实现非固定帧动画

我们知道，WebGL有两种Shader，分别是顶点着色器和片元着色器，它们都可以用来实现动画。我们先来看顶点着色器是怎么实现动画的。

attribute vec2 a_vertexPosition;
    attribute vec2 uv;
    
    varying vec2 vUv;
    uniform float rotation;
    
    void main() {
      gl_PointSize = 1.0;
      vUv = uv;
      float c = cos(rotation);
      float s = sin(rotation);
      mat3 transformMatrix = mat3(
        c, s, 0,
        -s, c, 0,
        0, 0, 1
      );
      vec3 pos = transformMatrix * vec3(a_vertexPosition, 1);
      gl_Position = vec4(pos, 1);
    }

在顶点着色器中，我们先绘制出一个红色的正方形，然后用三维齐次矩阵实现旋转。具体来说，就是把顶点坐标进行矩阵运算，再配合下面的JavaScript代码，就能让这个正方形旋转了。

renderer.uniforms.rotation = 0.0;
    
    requestAnimationFrame(function update() {
      renderer.uniforms.rotation += 0.05;
      requestAnimationFrame(update);
    });

当然，我们也可以使用上一节课得到的标准动画模型来实现。具体来说，就是定义一个新的Animator对象，然后在Animator对象的方法中更新rotation属性。使用标准模型能更加精确地控制图形的旋转效果，代码如下：

const animator = new Animator({duration: 2000, iterations: Infinity});
    animator.animate(renderer, ({target, timing}) => {
      target.uniforms.rotation = timing.p * 2 * Math.PI;
    });

总之，WebGL实现非固定帧动画的方法与上节课的方式基本上一样。只不过，前一节课我们直接修改HTML元素的属性，而这一节课我们将属性通过uniform变量传给着色器执行渲染。

2. 用片元着色器实现非固定帧动画

除了用顶点着色器，我们也能用片元着色器实现动画。实际上，我们已经用片元着色器实现了不少动画。比如说，当我们将时间参数uTime通过uniform传给着色器的时候，就是在实现动画。

还是用上面的例子。这次，我们将旋转放到片元着色器中处理，其实也能实现类似的旋转效果。代码如下所示：

#ifdef GL_ES
    precision highp float;
    #endif
    
    varying vec2 vUv;
    uniform vec4 color;
    uniform float rotation;
    
    void main() {
      vec2 st = 2.0 * (vUv - vec2(0.5));
      float c = cos(rotation);
      float s = sin(rotation);
      mat3 transformMatrix = mat3(
        c, s, 0,
        -s, c, 0,
        0, 0, 1
      );
      vec3 pos = transformMatrix * vec3(st, 1.0);
      float d1 = 1.0 - smoothstep(0.5, 0.505, abs(pos.x));
      float d2 = 1.0 - smoothstep(0.5, 0.505, abs(pos.y));
      gl_FragColor = d1 * d2 * color;
    }

你发现了吗，顶点着色器和片元着色器实现的旋转动画方向正好相反。为什么会出现这样的情况呢？因为在顶点着色器中，我们直接改变了顶点坐标，所以这样实现的旋转动画和WebGL坐标系（右手系）的方向一致，角度增大呈逆时针方向旋转。而在片元着色器中，我们的绘制原理是通过距离场着色来实现的，所以这里的旋转实际上改变的是距离场的角度而不是图形角度，最终绘制的图形也是相对于距离场的。又因为距离场逆时针旋转，所以图形就顺时针旋转了。

最后我再补充一点，一般来说，动画如果能使用顶点着色器实现，我们会尽量在顶点着色器中实现。因为在绘制一帧画面的时候，顶点着色器的运算量会大大少于片元着色器，所以使用顶点着色器消耗的性能更少。

但是，在片元着色器中实现非固定帧动画也有优势。我们可以使用片元着色器的技巧，如重复、随机、噪声等等来绘制更加复杂的效果。

比如说，我们把上面的代码稍微修改一下，使用取小数和取整数的函数，再用之前网格化的思路，来利用网格实现了大量的重复动画。这个做法充分利用了GPU的并行效率，比用其他方式把图形一个一个地绘制出来性能要高得多。

#ifdef GL_ES
    precision highp float;
    #endif
    
    varying vec2 vUv;
    uniform float rotation;
    
    float random (vec2 st) {
        return fract(sin(dot(st.xy,
                            vec2(12.9898,78.233)))*
            43758.5453123);
    }
    
    vec3 hsb2rgb(vec3 c){
      vec3 rgb = clamp(abs(mod(c.x*6.0+vec3(0.0,4.0,2.0), 6.0)-3.0)-1.0, 0.0, 1.0);
      rgb = rgb * rgb * (3.0 - 2.0 * rgb);
      return c.z * mix(vec3(1.0), rgb, c.y);
    }
    
    void main() {
      vec2 f_uv = fract(vUv * 10.0);
      vec2 i_uv = floor(vUv * 10.0);
      vec2 st = 2.0 * (f_uv - vec2(0.5));
      float c = 0.7 * cos(rotation);
      float s = 0.7 * sin(rotation);
      mat3 transformMatrix = mat3(
        c, s, 0,
        -s, c, 0,
        0, 0, 1
      );
      vec3 pos = transformMatrix * vec3(st, 1.0);
      float d1 = 1.0 - smoothstep(0.5, 0.505, abs(pos.x));
      float d2 = 1.0 - smoothstep(0.5, 0.505, abs(pos.y));
      gl_FragColor = d1 * d2 * vec4(hsb2rgb(vec3(random(i_uv), 1.0, 1.0)), 1.0);
    }

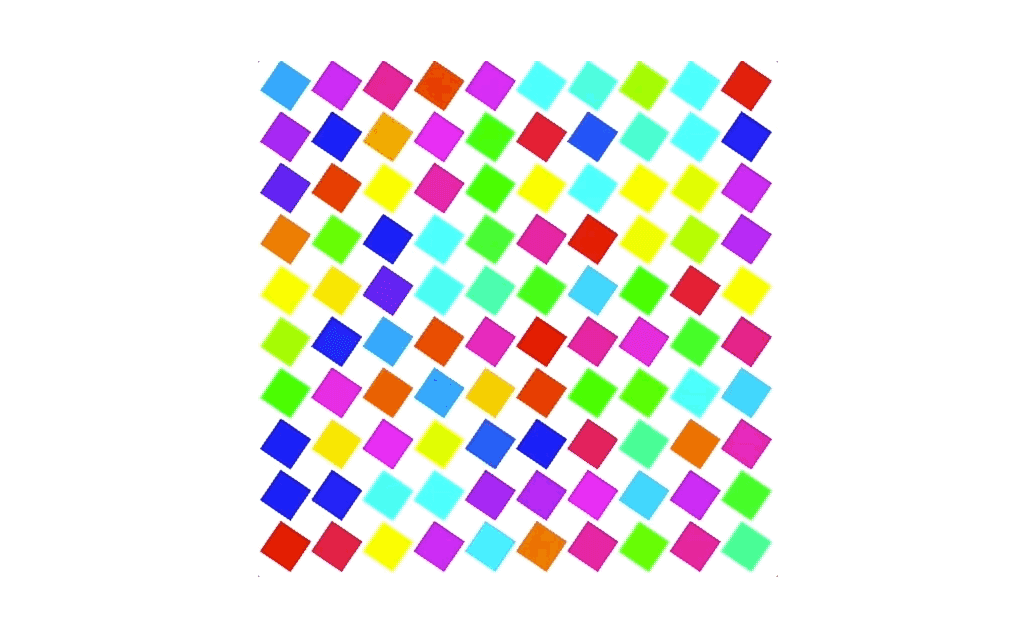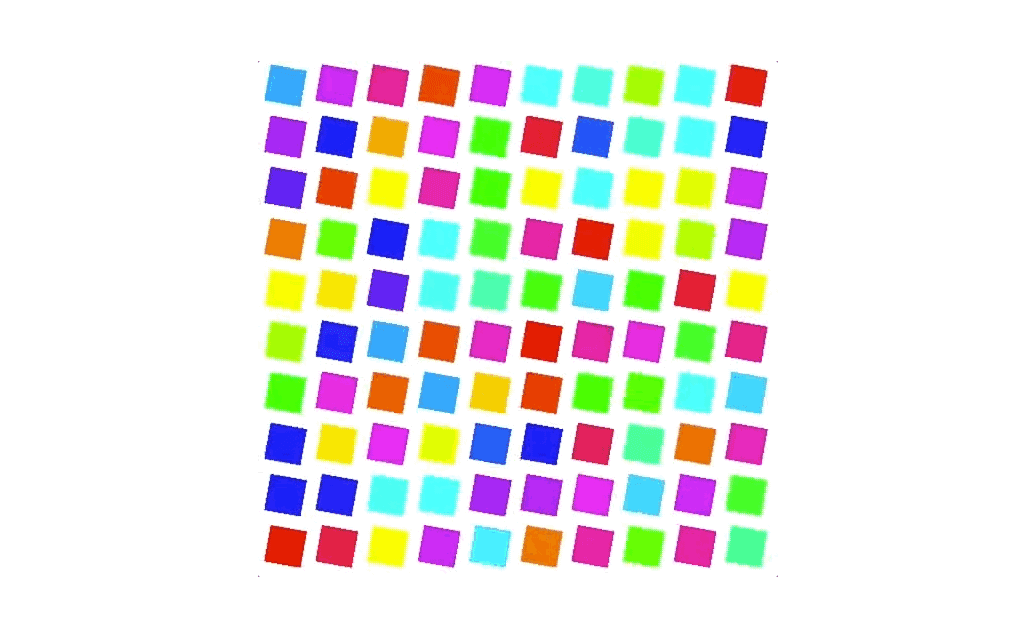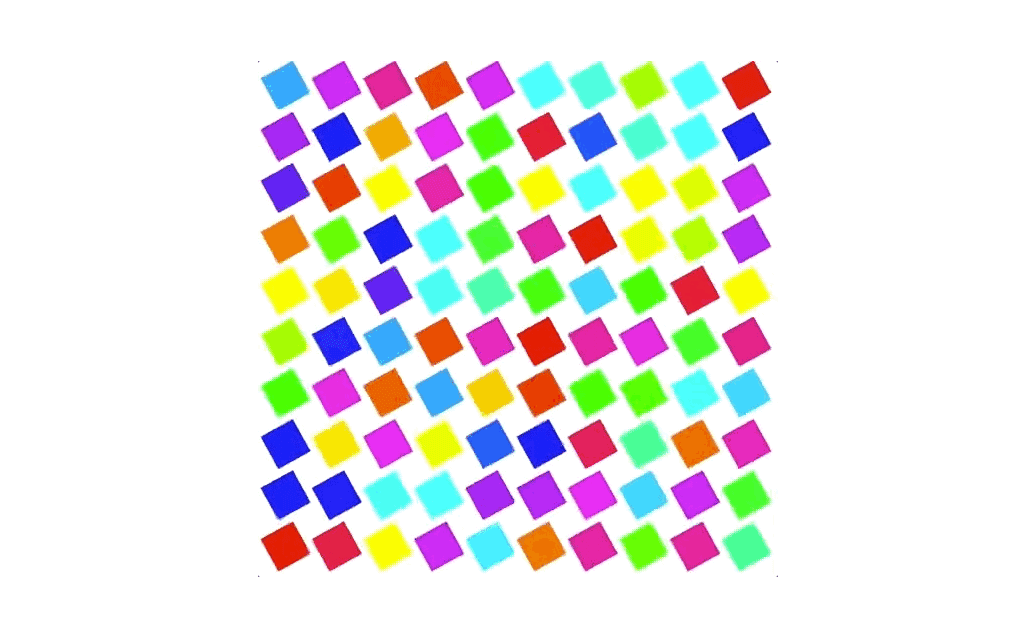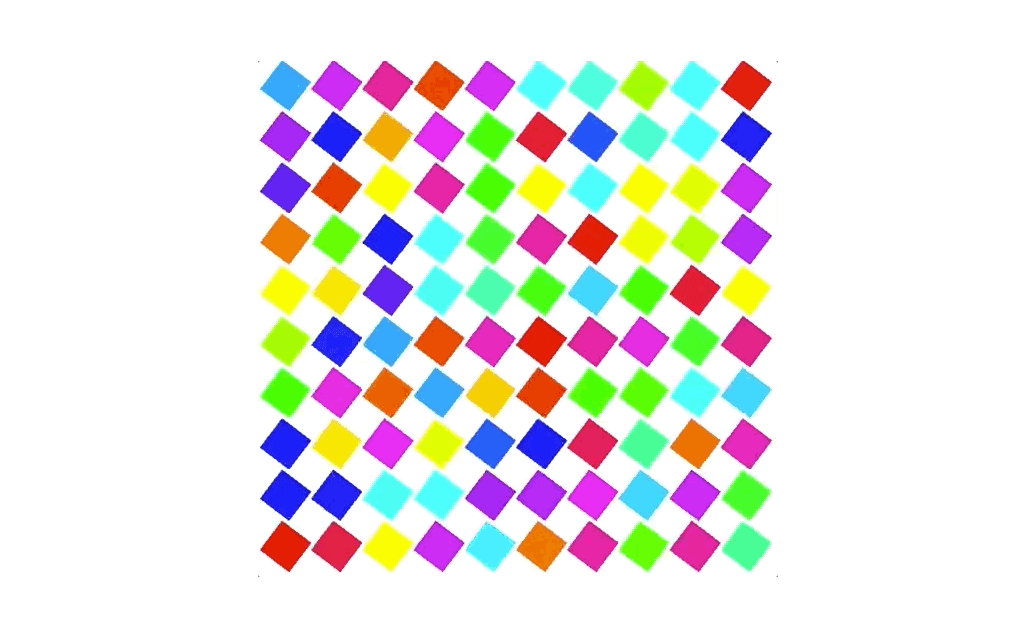
如何在着色器中实现缓动函数与非线性插值

在前面的例子中，我们使用Shader的矩阵运算实现了旋转动画。同样，轨迹动画也可以用Shader矩阵运算实现。

比如说，我们要在画布上绘制一个红色的方块，利用它实现轨迹动画。首先，我们要实现一个着色器，它通过设置translation来改变图形位置，代码如下：

attribute vec2 a_vertexPosition;
    attribute vec2 uv;
    
    varying vec2 vUv;
    uniform vec2 translation;
    
    void main() {
      gl_PointSize = 1.0;
      vUv = uv;
      mat3 transformMatrix = mat3(
        1, 0, 0,
        0, 1, 0,
        translation, 1
      );
      vec3 pos = transformMatrix * vec3(a_vertexPosition, 1);
      gl_Position = vec4(pos, 1);
    }

然后，在JavaScript中，我们将translation依照时间变化传给上面的着色器，就可以让方块移动。那利用下面的代码，我们就让方块沿水平方向向右匀速运动一段距离。

const canvas = document.querySelector('canvas');
    const renderer = new GlRenderer(canvas);
    const program = renderer.compileSync(fragment, vertex);
    renderer.useProgram(program);
    renderer.uniforms.color = [1, 0, 0, 1];
    renderer.uniforms.translation = [-0.5, 0];
    
    const animator = new Animator({duration: 2000});
    animator.animate(renderer, ({target, timing}) => {
      target.uniforms.translation = [-0.5 * (1 - timing.p) + 0.5 * timing.p, 0];
    });
    
    renderer.setMeshData([{
      positions: [
        [-0.25, -0.25],
        [-0.25, 0.25],
        [0.25, 0.25],
        [0.25, -0.25],
      ],
      attributes: {
        uv: [
          [0, 0],
          [0, 1],
          [1, 1],
          [1, 0],
        ],
      },
      cells: [[0, 1, 2], [2, 0, 3]],
    }]);
    renderer.render();

此外，我们还可以通过缓动函数来实现非匀速运动。而且我们既可以将缓动函数用JavaScript计算，也可以直接将缓动函数放在Shader中。如果将缓动函数用JavaScript计算，那么方法和上一节课完全一样，也就是给Animator传一个easing函数进去就可以了，这里我就不再重复了。但如果要将缓动函数写在Shader中，其实方法也非常简单。

我们以前面顶点着色器实现非固定帧动画的代码为例，这次，我们不使用Animator，而是直接将时间uTime参数传入Shader，然后在Shader中加入缓动函数。在这里，我们用smooth(0.0, 1.0, p)来让方块做平滑加速、减速运动。除此之外，你也可以替换缓动函数，比如clamp(p * p, 0.0, 1.0)或者clamp(p * (2 - p) * 0.0, 1.0)来实现匀加速、匀减速的运动效果。修改后的代码如下：

attribute vec2 a_vertexPosition;
    attribute vec2 uv;
    
    varying vec2 vUv;
    uniform vec4 uFromTo;
    uniform float uTime;
    
    float easing(in float p) {
      return smoothstep(0.0, 1.0, p);
      // return clamp(p * p, 0.0, 1.0);
      // return clamp(p * (2 - p) * 0.0, 1.0);
    }
    
    void main() {
      gl_PointSize = 1.0;
      vUv = uv;
      vec2 from = uFromTo.xy;
      vec2 to = uFromTo.zw;
      float p = easing(uTime / 2.0);
      vec2 translation = mix(from, to, p);
      mat3 transformMatrix = mat3(
        1, 0, 0,
        0, 1, 0,
        translation, 1
      );
      vec3 pos = transformMatrix * vec3(a_vertexPosition, 1);
      gl_Position = vec4(pos, 1);
    }

总之，因为Shader是在GPU中运算的，所以所有顶点都是被并行处理的。因此，通常情况下，我们在顶点着色器中执行缓动函数会更快。

不过，直接用JavaScript计算和放在顶点着色器里计算，差别也不是很大，但如果把它放在片元着色器里计算，因为要把每个像素点都计算一遍，所以性能消耗反而更大一些。那我们为什么还要在着色器中计算easing呢？这是因为，我们不仅可以利用easing控制动画过程，还可以在片元着色器中用easing来实现非线性的插值。

那什么是非线性插值呢？我们依然通过例子来进一步理解。

我们知道，在正常情况下，顶点着色器定义的变量在片元着色器中，都会被线性插值。比如，你可以看我下面给出的顶点着色器、片元着色器，以及JavaScript中的代码。

//顶点着色器
    attribute vec2 a_vertexPosition;
    attribute vec2 uv;
    attribute vec4 color;
    
    varying vec2 vUv;
    varying vec4 vColor;
    uniform vec4 uFromTo;
    uniform float uTime;
    
    void main() {
      gl_PointSize = 1.0;
      vUv = uv;
      vColor = color;
      gl_Position = vec4(a_vertexPosition, 1, 1);
    }
    
    //片元着色器
    
    #ifdef GL_ES
    precision highp float;
    #endif
    
    varying vec2 vUv;
    varying vec4 vColor;
    
    void main() {
      gl_FragColor = vColor;
    }
    
    //JavaScript中的代码
    renderer.setMeshData([{
      positions: [
        [-0.5, -0.25],
        [-0.5, 0.25],
        [0.5, 0.25],
        [0.5, -0.25],
      ],
      attributes: {
        uv: [
          [0, 0],
          [0, 1],
          [1, 1],
          [1, 0],
        ],
        color: [
          [1, 0, 0, 1],
          [1, 0, 0, 1],
          [0, 0.5, 0, 1],
          [0, 0.5, 0, 1],
        ],
      },
      cells: [[0, 1, 2], [2, 0, 3]],
    }]);
    renderer.render();

通过执行上面的代码，我们可以得到一个长方形，它的颜色会从左到右，由红色线性地过渡到绿色。如果想要实现非线性的颜色过渡，我们就不能采用这种方式了，我们可以采用uniform的方式，通过easing函数来实现。

#ifdef GL_ES
    precision highp float;
    #endif
    
    float easing(in float p) {
      return smoothstep(0.0, 1.0, p);
      // return clamp(p * p, 0.0, 1.0);
      // return clamp(p * (2 - p) * 0.0, 1.0);
    }
    
    varying vec2 vUv;
    uniform vec4 fromColor;
    uniform vec4 toColor;
    
    void main() {
      float d = easing(vUv.x);
      gl_FragColor = mix(fromColor, toColor, d);
    }

比如，我们可以使用smoothstep这种easing函数，来实现如下的插值效果：

另外，我们还可以像利用JavaScript那样，在Shader里实现贝塞尔曲线缓动。

// http://www.flong.com/texts/code/shapers_bez/
    // Helper functions:
    float slope_from_t (float t, float A, float B, float C){
      float dtdx = 1.0/(3.0*A*t*t + 2.0*B*t + C); 
      return dtdx;
    }
    
    float x_from_t (float t, float A, float B, float C, float D){
      float x = A*(t*t*t) + B*(t*t) + C*t + D;
      return x;
    }
    
    float y_from_t (float t, float E, float F, float G, float H){
      float y = E*(t*t*t) + F*(t*t) + G*t + H;
      return y;
    }
    
    float cubic_bezier (float x, float a, float b, float c, float d){
      float y0a = 0.00; // initial y
      float x0a = 0.00; // initial x 
      float y1a = b;    // 1st influence y   
      float x1a = a;    // 1st influence x 
      float y2a = d;    // 2nd influence y
      float x2a = c;    // 2nd influence x
      float y3a = 1.00; // final y 
      float x3a = 1.00; // final x 
    
      float A = x3a - 3.0 *x2a + 3.0 * x1a - x0a;
      float B = 3.0 * x2a - 6.0 * x1a + 3.0 * x0a;
      float C = 3.0 * x1a - 3.0 * x0a;   
      float D = x0a;
    
      float E = y3a - 3.0 * y2a + 3.0 * y1a - y0a;    
      float F = 3.0 * y2a - 6.0 * y1a + 3.0 * y0a;             
      float G = 3.0 * y1a - 3.0 * y0a;             
      float H = y0a;
    
      // Solve for t given x (using Newton-Raphelson), then solve for y given t.
      // Assume for the first guess that t = x.
      float currentt = x;
      const int nRefinementIterations = 5;
      for (int i=0; i < nRefinementIterations; i++){
        float currentx = x_from_t(currentt, A,B,C,D); 
        float currentslope = slope_from_t(currentt, A,B,C);
        currentt -= (currentx - x)*(currentslope);
        currentt = clamp(currentt, 0.0, 1.0);
      } 
    
      float y = y_from_t(currentt, E,F,G,H);
      return y;
    }

使用贝塞尔曲线缓动函数，我们能够实现更加丰富多彩的插值效果。

如何在片元着色器中实现随机粒子动画

我们知道，使用片元着色器还可以实现非常复杂的图形动画，包括粒子动画、网格动画以及网格噪声动画等等。网格动画和网格噪声我们前面都详细讲过，这里我们就重点来说说怎么实现粒子动画效果。

#ifdef GL_ES
    precision highp float;
    #endif
    
    ...
    
    float sdf_circle(vec2 st, vec2 c, float r) {
      return 1.0 - length(st - c) / r;
    }
    
    varying vec2 vUv;
    uniform float uTime;
    
    void main() {
      vec2 st = vUv;
      float rx = mix(-0.2, 0.2, noise(vec2(7881.32, 0) + random(st) + uTime));
      float ry = mix(-0.2, 0.2, noise(vec2(0, 1433.59) + random(st) + uTime));
      float dis = distance(st, vec2(0.5));
      dis = pow((1.0 - dis), 2.0);
      float d = sdf_circle(st + vec2(rx, ry), vec2(0.5), 0.2);
      d = smoothstep(0.0, 0.1, d);
      gl_FragColor = vec4(dis * d * vec3(1.0), 1.0);
    }

如上面代码所示，我们可以使用随机+噪声来实现一个粒子效果。首先，我们设置随机数用来生成距离场的初始值，然后设置噪声用来形成位移，最后传入uTime变量来实现动画。

这样一来，我们就能绘制出数量非常多的点，并且让它们沿着随机轨迹运动。最终的视觉效果如下：

像这样流畅的动画效果，因为实现的过程中会涉及非常多点的运算，如果不用shader，我们几乎是无法完成的。

要点总结

这节课我们学习了用WebGL实现动画的方法。

如果是实现固定帧动画，在WebGL中，我们可以把准备好的图片作为纹理，然后动态修改纹理坐标。

如果是实现非固定帧动画，我们可以通过uniform，将变化的属性作为参数传给着色器处理。上节课的标准动画模型在WebGL中依然可以使用，我们可以利用它计算出属性，再传入着色器执行渲染。

实际上，今天讲的方法，与用HTML/CSS、SVG、Canvas2D实现动画的基本原理是一样的。只不过，WebGL中的很多计算，是需要用JavaScript和GLSL，也就是Shader来配合进行的。

这节课的实战例子比较多，我建议你好好研究一下。毕竟，使用片元着色器实现动画效果的思路，我们还会在后续课程中经常用到。

小试牛刀

今天，我们在Shader中通过矩阵运算实现了图形的旋转和平移，你能用学到的知识完善矩阵运算，来实现缩放、旋转、平移和扭曲变换，以及它们的组合效果吗？
结合今天的内容，你可以试着实现一个粒子效果：让一张图片从中心爆炸开来，炸成碎片并最终消失。

欢迎在留言区和我讨论，分享你的答案和思考，也欢迎你把这节课分享给你的朋友，我们下节课见！

源码

本节课完整示例代码见GitHub仓库

大师兄