10 | 解析几何:为什么说它是向量从抽象到具象的表达?
你好,我是朱维刚。欢迎你继续跟我学习线性代数,今天我们要讲的内容是“解析几何”。
前面所有章节我们都是围绕向量、矩阵,以及向量空间来展开的。但这一节课有点不一样,我要讲的是解析几何,它使得向量从抽象走向了具象,让向量具有了几何的含义。比如,计算向量的长度、向量之间的距离和角度,这在机器学习的主成分分析PCA中是非常有用的。
范数
讲解析几何我们得从“范数”开始讲起。
因为很多人看到几何向量的第一反应就是,它是从原点开始的有向线段,并且向量的长度是这个有向线段的终端和起始端之间的距离。而范数,就是被用来度量某个向量空间或矩阵中的每个向量的长度或大小的。
现在,我们先来看一下范数的数学定义:一个向量空间$V$上的一个范数就是一个函数,它计算$V$中的每一个向量$x$的长度,用符号来表示的话就是:$\|x\| \in R$,它满足三种性质:
- 正齐次性: 如果输入参数扩大正$λ$倍,其对应的函数也扩正大倍。设$λ \in R$,$x \in V$,$\|\lambda x\|=|\lambda|\|x\|$;
- 次可加性:类似三角不等式,两边之和大于第三边。设$x,y \in V$,$\|x+y\| \leq\|x\|+\|y\|$;
- 正定性:向量$x$的长度一定大于等于零。$\|x\| \geq 0$。
看到这里,你也许会问,范数似乎和以前老师教的向量的模一样啊。先别急,它们还真有那么一点关系,你听我慢慢道来。由于范数是度量某个向量空间或矩阵中的每个向量的长度或大小的,所以它和向量空间维度是有关系的,于是,我们可以把范数写成这样的模式来区分不同维度的大小计算:$L_{1}, L_{2}, \ldots, L_{\infty}$。
- $L_{1}$范数:曼哈顿范数,也叫曼哈顿距离,设$x \in R^{n}$,得到下面这个表达式。
$$
\|x\|_{1}=\sum_{i=1}^{n}\left|x_{i}\right|
$$
- $L_{2}$范数:欧式范数,也叫欧式距离,设$x \in R^{n}$,得到下面这个表达式。
$$
\|x\|_{2}=\sqrt{\sum_{i=1}^{n} x_{i}^{2}}
$$
- $L_{\infty}$范数:切比雪夫范数,也叫切比雪夫距离,设$x \in R^{n}$,得到下面这个表达式。
$$
\|x\|_{\infty}=\max \left(\left|x_{1}\right|,\left|x_{2}\right|, \ldots,\left|x_{n}\right|\right)
$$
我们发现,向量的模和$L_{2}$范数的计算方式都是一样的,都表示的是欧氏距离,所以,我们可以简单地认为向量的模等于$L_{2}$范数。而其他的范数模式和向量的模则没有任何关系。
内积
学习解析几何时,我们必须掌握的第二个概念就是内积。
如果说范数是模式,是用来描述向量长度或大小的概念性表达,那么内积可以让我们很直观地了解一个向量的长度、两个向量之间的距离和角度,它的一个主要目的就是判断向量之间是否是正交的,正交这个概念我们会在后面讲解。
点积
我们从特殊到一般,先来看点积,它和第三篇矩阵中说的“普通矩阵乘”形式一样,点积是特殊的内积,为什么说它特殊呢?那是因为在表示两个向量之间的距离时,它就是大家熟悉的欧式距离,点积可以表示成这样的形式:
$$
x^{T} y=\sum_{i=1}^{n} x_{i} y_{i}
$$
其他内积
除了点积外,我们再来看另一个不同的内积:设内积空间$V$是$R^{2}$,定义内积$\langle x, y\rangle=x_{1} y_{1}-(x_{1} y_{2}+x_{2} y_{1})+2 x_{2} y_{2}$,一看便知这个和点积完全不同。
内积空间
最后,我们再来看一般内积和内积空间。因为解析几何关注的是向量的长度、两个向量之间的距离和角度,所以,我们要在原来向量空间上加一个额外的结构,这个额外结构就是内积,而加了内积的向量空间,我们就叫做内积空间。
为了表达方便,我们可以把内积写成$\langle\ ·,· \rangle$这样的形式,那么内积空间$V$可以被表示成这样:$(V,\langle\ ·,· \rangle)$。这时,如果一般内积由点积来表达,那这个向量空间就变成了更具体的欧式向量空间。
接下来看下内积空间有什么性质?我们定义一个内积空间V和它的元素$x$、$y$、$z$,以及一个$c \in R$:
满足对称性:$x$和$y$的内积等于$y$和$x$的内积,$\langle x, y\rangle=\langle y, x\rangle$;
满足线性性:$x$和$y+cz$的内积等于,$x$和$y$的内积,与$x$和$z$的内积乘以$c$后的和,
$\langle x, y+c z\rangle=\langle x, y\rangle+c\langle x, z\rangle$;满足正定性:$x$和$y$的内积大于等于零,$\langle x, y\rangle \geq 0$。
对称正定矩阵
内积还定义了一类矩阵,这类矩阵在机器学习中很重要,因为它可以被用来判定多元函数极值,而在深度学习中,它更是被用来获取最小化损失函数,我们把这类矩阵叫做对称正定矩阵。
对称正定矩阵的定义是:如果一个对称矩阵$A$属于方阵$R^{n×n}$,对任意非零向量$x$,都有$x^{T} A x>0$,那么$A$就是对称正定矩阵。
我们来看两个例子,判断它们是不是对称正定矩阵。
第一个例子,请你回答下面这个矩阵是对称正定矩阵吗?
$$
A=\left[\begin{array}{ll}
9 & 6 \\\
6 & 5
\end{array}\right]
$$
答案:是的,它是对称正定矩阵。因为$x^{T} A x>0$。
$$
x^{T} A x=\left[\begin{array}{ll}
x_{1} & x_{2}
\end{array}\right]\left[\begin{array}{ll}
9 & 6 \\\
6 & 5
\end{array}\right]\left[\begin{array}{l}
x_{1} \\\
x_{2}
\end{array}\right]=(3 x_{1}+2 x_{2})^{2}+x_{2}^{2}>0
$$
第二个例子,请你看下面这个矩阵是对称正定矩阵吗?
$$
A=\left[\begin{array}{ll}
9 & 6 \\\
6 & 3
\end{array}\right]
$$
答案:不是的,它只是对称矩阵。因为$x^{T} A x$可能小于0。
$$
x^{T} A x=\left[\begin{array}{ll}
x_{1} & x_{2}
\end{array}\right]\left[\begin{array}{ll}
9 & 6 \\\
6 & 3
\end{array}\right]\left[\begin{array}{l}
x_{1} \\\
x_{2}
\end{array}\right]=(3 x_{1}+2 x_{2})^{2}-x_{2}^{2}
$$
长度、距离和角度
前面我们通过范数讲了向量的长度,但从内积的角度来看,我们发现,内积和范数之间有着千丝万缕的关系。我们来看看下面这个等式。
$$
\|x\|=\sqrt{\langle x, x\rangle}
$$
从这个等式我们发现,内积可以用来产生范数,确实是这样。不过,不是每一个范数都能被一个内积产生的,比如:曼哈顿范数。接下来,我们还是来关注能由内积产生的范数上,从不同的角度来看看几何上的长度、距离和角度的概念。
我们先用内积来计算一个向量的长度,比如:向量$x=[\begin{array}{ll}1 & 1\end{array}]^{T}$,我们可以使用点积来计算,计算后得出$x$的范数是$\sqrt{2}$,具体计算过程是这样的:$\|x\|=\sqrt{x^{T} x}=\sqrt{1^{2}+1^{2}}=\sqrt{2}$。
接着,我们再来看一下向量之间的距离,一个内积空间$V$,$(V,\langle\ ·,· \rangle)$,$x$和$y$是它的两个向量,那么$x$和$y$之间的距离就可以表示成:$d(x, y)=\|x-y\|=\sqrt{\langle x-y, x-y\rangle}$。
如果用点积来计算$x$和$y$之间的距离,那这个距离就叫做欧式距离。
再接着,来看看两个向量之间的角度。我们使用柯西-施瓦茨不等式(Cauchy-Schwarz Inequality)来表示内积空间中两个向量$x$和$y$之间的角度:$a$。
$$
-1 \leq \frac{\langle x, y\rangle}{\|x\|\|y\|} \leq 1
$$
取值是从$-1$到$1$之间,那么角度就是从$0$到$π$之间,我们用$cos$来表示就是:
$$
\cos (a)=\frac{\langle x, y\rangle}{\|x\|\|y\|}
$$
其中$a$就是角度,$a$的角度取值是$0$到$π$之间。我们很容易就能发现,其实两个向量之间的角度,就是告诉了我们两个向量之间方向的相似性。例如:$x$和$y=4x$,使用点积来计算它们之间的角度是$0$,也就是说它们的方向是一样的,$y$只是对$x$扩大了$4$倍而已。
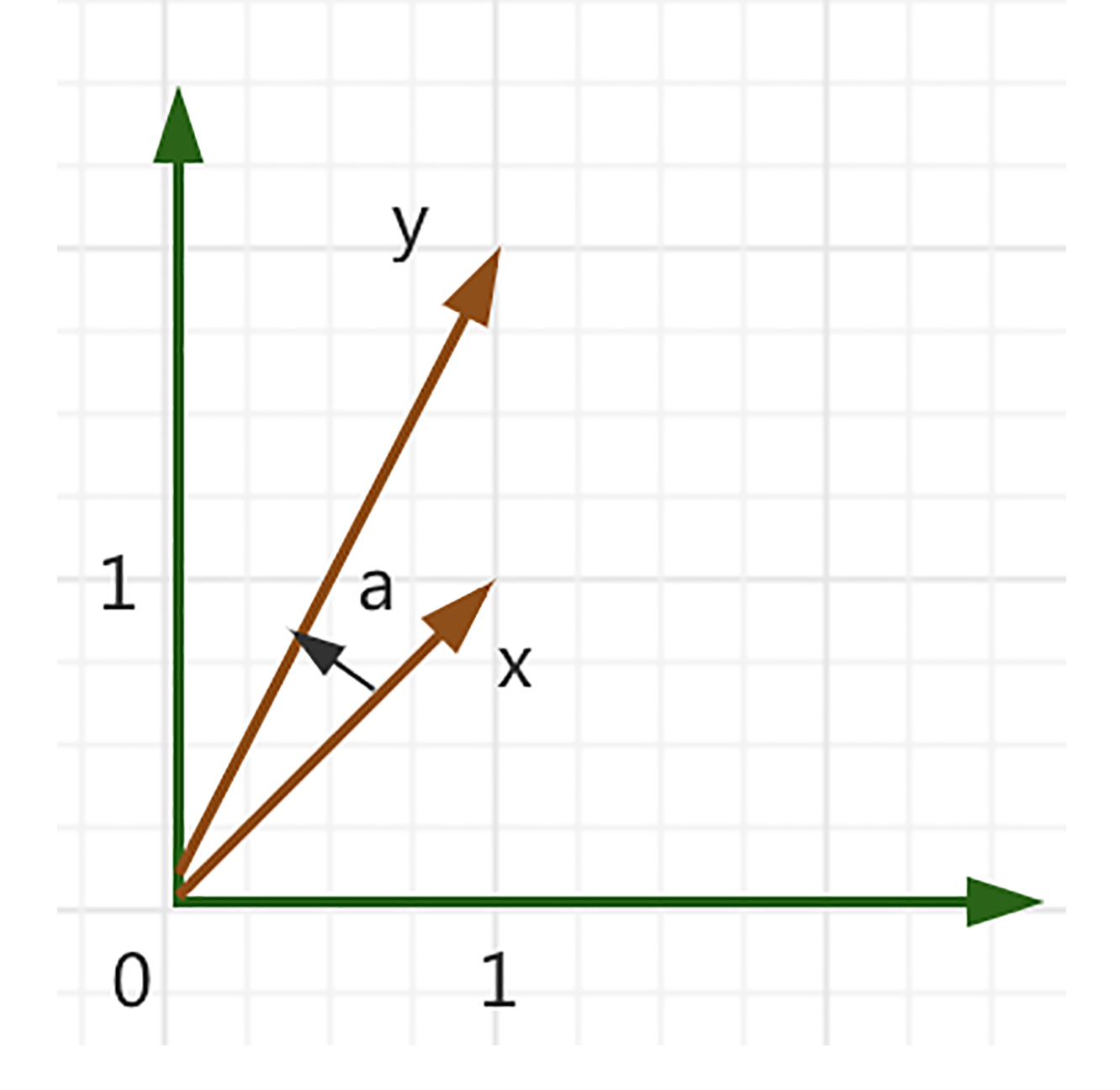
现在,我们通过一个例子,再来更清楚地看下两个向量之间角度的计算,设$x=[\begin{array}{ll}1 & 1\end{array}]^{T}$,$y=[\begin{array}{ll}1 & 2\end{array}]^{T}$,使用点积来计算,我们得出:
$$
\cos (a)=\frac{\langle x, y\rangle}{\sqrt{\langle x, x\rangle\langle y, y\rangle}}=\frac{x^{T} y}{\sqrt{x^{T} x y^{T} y}}=\frac{3}{\sqrt{10}}
$$
那么,这两个向量之间的角度如下。
$$
\arccos \left(\frac{3}{\sqrt{10}}\right) \approx 0.32
$$
我们可以用图来更直观地表达一下。
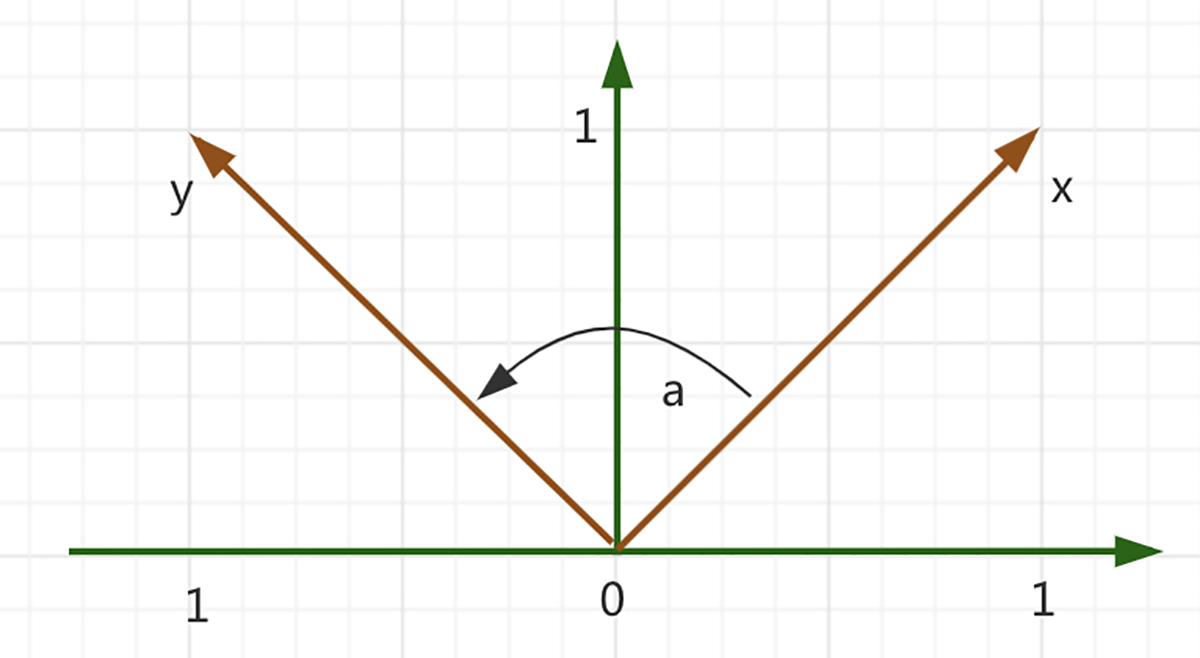
于是,我们最后可以引出一个概念,也就是我们在一开始提到的正交性。如果两个向量$x$和$y$内积等于$0$,$\langle x, y\rangle=0$,那么$x$和$y$是正交的,这可以写成:$x \perp y$。再如果,$x$和$y$的范数都等于$1$,$\|x\|=\|y\|=1$,也就是说,如果它们都是单位向量,那么$x$和$y$就是标准正交的。
我们用图来更直观地表达一下。
正交投影
在理论讲解之后,我们要来了解一下解析几何在实践中经常运用的概念——正交投影,它是一种重要的线性变换,在图形图像、编码理论、统计和机器学习中扮演了重要角色。
在机器学习中,数据一般都是高维的。众所周知,高维数据是很难来分析和可视化的。而且,不是所有的高维数据都是有用的,可能只有一些数据包含了大部分的重要信息。
正交投影就是高维到低维的数据投影,在第5节课线性空间中,我简单介绍了高维数据投影到低维后,我们就能在低维空间更多地了解数据集、提炼相关模式。而在机器学习中,最普遍的降维算法——PCA主成分分析,就是利用了降维的观点。
接下来,我开始讲解正交投影,在给出定义之前,先从一张图来了解会更直观。
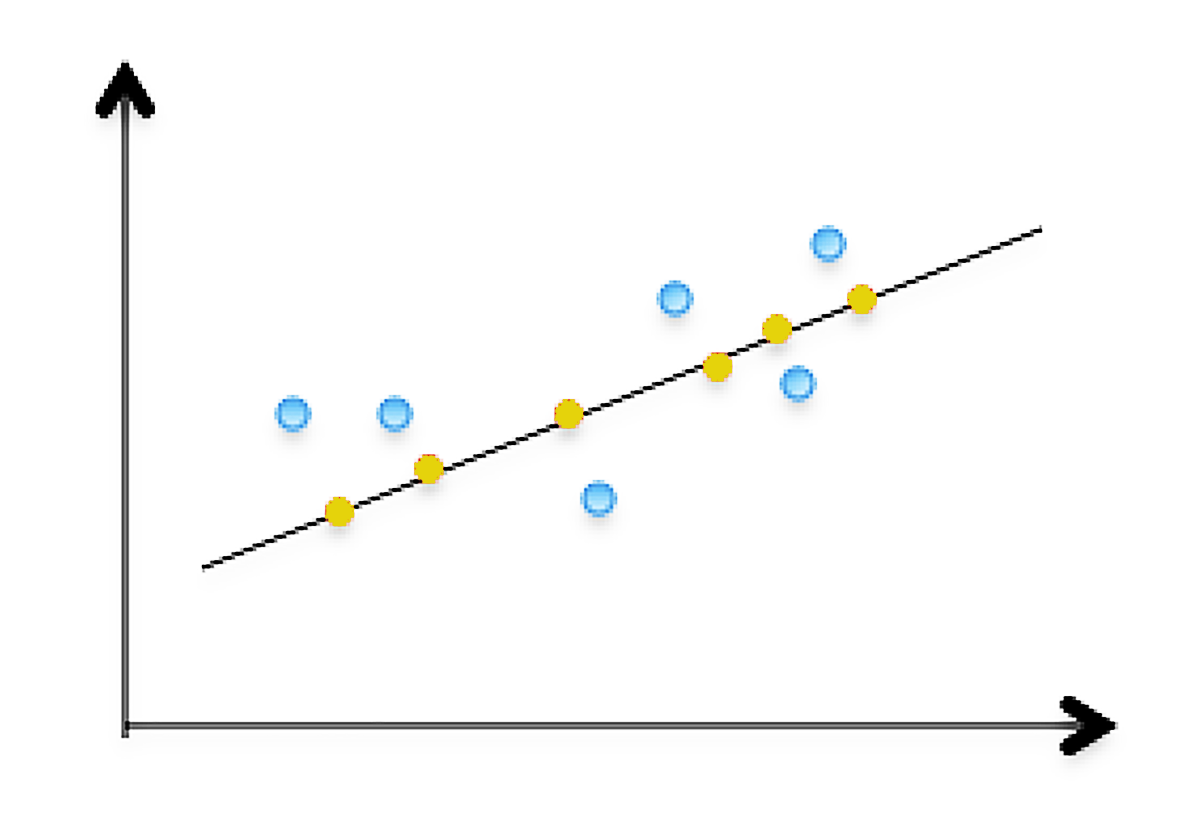
图中的蓝点是原二维数据,黄点是它们的正交投影。所以,实际降维后,在一维空间中就形成了这条黑线表示,它近似地表达了原来二维数据表示的信息。
现在我们可以来看一下投影的定义:$V$是一个向量空间,$U$是$V$的一个向量子空间,一个从$V$到$U$的线性映射$\Phi$是一个投影,如果它满足:$\Phi^{2}=\Phi \circ \Phi=\Phi$。因为线性映射能够被变换矩阵表示,所以,这个定义同样适用于一个特殊类型变换矩阵:投影矩阵$P_{\Phi}$,它也满足:$P_{\Phi}^{2}=P_{\Phi}$。
投影到一维子空间上(线)
接下来,我们来看看如何投影到一维子空间,也就是把内积空间的向量正交投影到子空间,这里我们使用点积作为内积。
假设有一条通过原点的线,这条线是由基向量$b$产生的一维子空间$U$,当我们把一个向量$x$投影到$U$时,需要寻找另一个最靠近$x$的向量$\Phi_{U}(x)$。还是老样子,我们通过图来看一下。
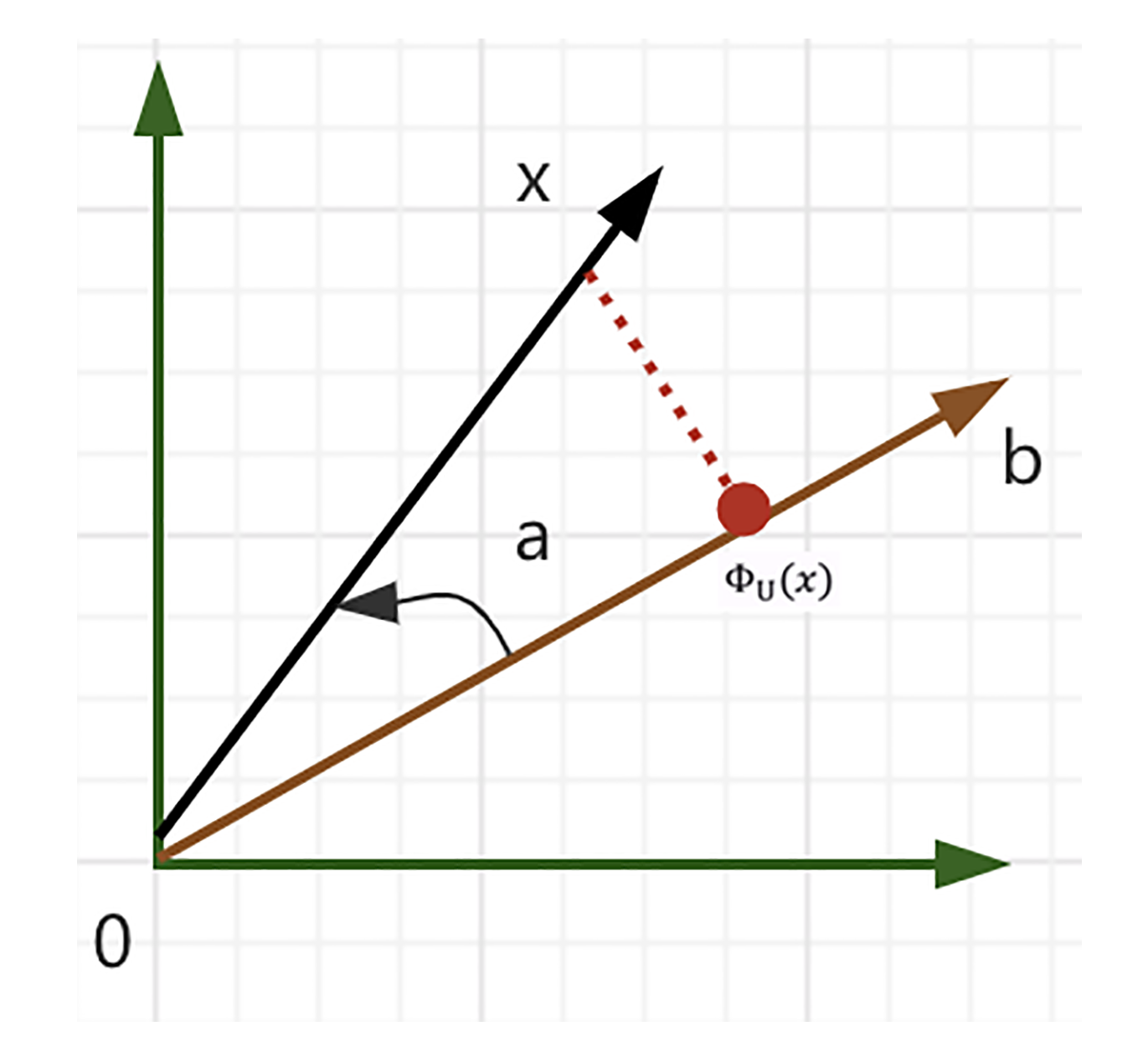
首先,投影$\Phi_{U}(x)$靠近$x$,也就是要找出$x$和$\Phi_{U}(x)$之间的$\left\|x-\Phi_{U}(x)\right\|$最小距离,从几何角度来说,就是线段$\Phi_{U}(x)-x$和$b$正交,满足等式:$\left\langle\Phi_{U}(x)-x, b\right\rangle=0$。其次,投影$\Phi_{U}(x)$必须是$U$的一个元素,也就是,基向量$b$的一个乘来产生$U$,$\Phi_{U}(x)=λb$。
于是,我们可以通过三个步骤来分别得到$λ$、投影$\Phi_{U}(x)$和投影矩阵$P_{\Phi}$,来把任意$x$映射到子空间$U$上。
第一步,计算$λ$,通过正交条件产生这样的等式:
$\left\langle x-\Phi_{U}(x), b\right\rangle=0$。因为$\Phi_{U}(x)=λb$,所以它可以转变成:$\langle x-\lambda b, b\rangle=0$。
利用内积的双线性:$\langle x, b\rangle-\lambda\langle b, b\rangle=0$,我们得到:
$$
\lambda=\frac{\langle x, b\rangle}{\langle b, b\rangle}=\frac{\langle b, x\rangle}{\|b\|^{2}}
$$
然后,我们通过点积得到:
$$
\lambda=\frac{b^{T} x}{\|b\|^{2}}
$$
如果$\|b\|=1$,那$λ$就等于$b^{T}x$。
接着第二步,是计算投影点$\Phi_{U}(x)$。从$\Phi_{U}(x)=λb$,我们得到:
$$
\Phi_{U}(x)=\lambda b=\frac{\langle x, b\rangle}{\|b\|^{2}} b=\frac{b^{T} x}{\|b\|^{2}} b
$$
通过点积来计算,我们就得到了$\Phi_{U}(x)$的长度:
$$
\left\|\Phi_{U}(x)\right\|=\frac{\left|b^{T} x\right|}{\|b\|^{2}}\|b\|=|\cos (a)|\|x\|\|b\| \frac{\|b\|}{\|b\|^{2}}=\mid \cos (a)\|x\|
$$
这里的$a$,是$x$和$b$之间的夹角。
最后第三步,是计算投影矩阵$P_{\Phi}$,投影矩阵是一个线性映射。所以,我们可以得到:$\Phi_{U}(x)=P_{\Phi}x$,通过$\Phi_{U}(x)=λb$,我们可以得到:
$$
\Phi_{U}(x)=\lambda b=b \lambda=b \frac{b^{T} x}{\|b\|^{2}}=\frac{b b^{T}}{\|b\|^{2}} x
$$
这里,我们立即可以得到投影矩阵$P_{\Phi}$的计算等式:
$$
P_{\Phi}=\frac{b b^{T}}{\|b\|^{2}}
$$
本节小结
这一节课覆盖的知识点有点多,因为要把解析几何的知识点,浓缩到核心的几个点来讲解是一项艰巨的任务。不过不要怕,前面的几个知识点都是为这一节的重点“正交投影”来铺垫的。范数,被用来度量某个向量空间或矩阵中的每个向量的长度或大小,而内积让我们很直观地了解一个向量的长度、两个向量之间的距离和角度,以及判断向量之间是否是正交的。
所以,希望你能掌握范数和内积的理论知识,并把它和正交投影结合,运用在一些实践应用场景中,比如:3D图形图像的坐标变换、数据压缩,以及机器学习的降维。
线性代数练习场
请用之前学到的正交投影的投影矩阵算法,来计算一条线上的投影矩阵$P_{\Phi}$。
这条线通过原点,由基$b=\left[\begin{array}{lll}1 & 2 & 2\end{array}\right]^{T}$产生,$P_{\Phi}$计算后,再通过一个$x$来验证一下它是否在$b$产生的子空间中,我们取$x=\left[\begin{array}{lll}1 & 1 & 1\end{array}\right]^{T}$。
欢迎在留言区晒出你的运算结果,我会及时回复。同时,也欢迎你把这篇文章分享给你的朋友,一起讨论、学习。